Aujourd'hui, retour de Porto Alegre. Plus de 10 heures d'avion jusqu'à Lisbonne dans un siège particulièrement inconfortable. Occupons-nous donc un peu… Il y a quelques temps, j'ai montré Sweave / knitr à Jean-Marc et je lui affirmais que ggplot2, c'était surpuissant et qu'une fois qu'on y avait goûté, on se demandait comment on avait pu faire sans et utiliser gnuplot. Comme Jean-Marc aime bien troller, il m'a dit qu'il avait bien essayé mais que c'était pénible comme tout et qu'on avait au final un bien meilleur contrôle avec ce bon vieux gnuplot retouché avec xfig. La preuve! Tsss… OK, challenge accepted! ;) Comme le débat ne porte pas vraiment sur knitr et qu'en ce moment, je suis en train de passer complètement à org-mode et babel, je vais me payer le luxe de faire plutôt un export html et poster sur mon "blog". ;) Enfin, comme je pense que prendre l'habitude de montrer le code qui permet d'arriver au résultat est important, j'exporte tout le code. Au final, on s'apperçoit que ce qui est annoncé dans le document initial de Jean-Marc, aussi joli soit-il, ne correspond pas parfaitement à ce qui est annoncé (ceci dit, le connaissant, il se peut que ça soit un choix pédagogique… ;).

Contexte

L'objectif est d'analyser l'importance de la distribution du temps de service sur le temps de réponse dans une file d'attente M/GI/1 avec un ordonnancement FIFO. Le processus d'arrivée est un processus de Poisson de taux λ (débit), les clients ont un temps de service de moyenne 1 pris comme unité de temps de référence.

Méthode

Simulation équationnelle à partir de la relation de récurrence sur les temps de réponse (équation de Lindley).

library(plyr)
library(ggplot2)
Service <- function(typeservice,x,y) {
# genere un temps de service
  switch(typeservice,
         det = 1,
         uni = runif(1,x,y),
         erl = rgamma(1,x,y),
         exp = rexp(1,x)
         )
}

Response <- function(n,lambda,typeservice,x,y) {
    # genere une trajectoire de temps de reponse pour une file M/GI/1 FIFO
    # parametres :
    #    n :  taille de la trajectoire
    #    lambda : debit d'arrivee
    #    typeservice : type de service (det uni erl exp)
    #    x ,y : parametres de la loi de service
    # valeur de retour :
    #    vecteur de n valeurs successives du temps de
    #    réponse dans une M/GI/1 FIFO initialement vide

    # generation des arrivees
    A <- rexp(n,lambda)
    t1 <- cumsum(A)

    # initialisation des structures
    t2 <- c(1:n)

    # initialisation du premier terme
    t2[1] <- t1[1]+ Service(typeservice,x,y)

    # calcul de la trajectoire equation de recurrence de Lindley
    for ( i in 2:n) {
        t2[i] <- Service(typeservice,x,y) + max(t1[i], t2[i-1])
    }
    t2-t1
}    


create <- function(n,lambda_min,lambda_max,step,typeservice,x,y) {
  d <- data.frame(n=1,lambda=0,response=1,sd=0)    
  for (lambda in seq(lambda_min,lambda_max,step)) {
    r <- Response(n,lambda,typeservice,x,y)
    d = rbind(d,data.frame(n=n,lambda=lambda,response=mean(r),sd=sd(r)))
  }
  d$input_type = typeservice
  d$input_p1 = x
  d$input_p2 = y
  d$label = as.factor(paste(typeservice,"(",x,",",y,")",sep=""))
  d
}

Plan d'expérience

Pour chaque loi et pour des valeurs de λ de 0 à 0.95 avec un pas de 0.01 on estime le temps de réponse moyen des clients sur des échantillons de taille N=10000.

experiment <- function(sample_size=10000) {
  resp_exp <-create(sample_size,0.01,0.95,0.01,"exp",1,0)
  resp_det <-create(sample_size,0.01,0.95,0.01,"det",0,0)
  resp_u02 <-create(sample_size,0.01,0.95,0.01,"uni",0,2)
  resp_u0.5_1.5 <-create(sample_size,0.01,0.95,0.01,"uni",0.5,1.5)
  resp_erl22 <-create(sample_size,0.01,0.95,0.01,"erl",2,2)
  resp_erl33 <-create(sample_size,0.01,0.95,0.01,"erl",3,3)
  rbind(resp_exp, resp_det, resp_u02, resp_u0.5_1.5, resp_erl22, resp_erl33)
}

Le résultat attendu

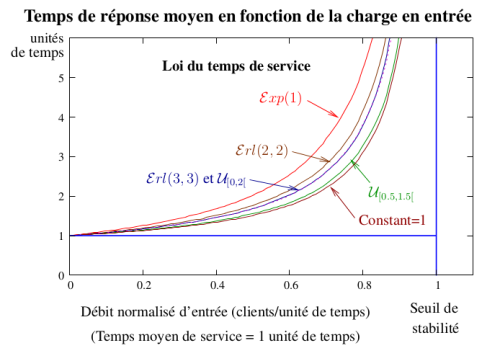
Voici ensuite, la figure qu'obtient Jean-Marc et ce qu'il en dit:

Les intervalles de confiance sont suffisamment petits pour ne pas être visualisés (les écarts entre les courbes sont significatifs). On effectue une interpolation entre les points par la méthode de Bézier.

Une variance plus grande que prévue…

À nous alors… Jetons un oeil à la structure de la data-frame ainsi crée

df<-experiment()
head(df)

      n lambda response       sd input_type input_p1 input_p2    label
1     1   0.00 1.000000 0.000000        exp        1        0 exp(1,0)
2 10000   0.01 1.011676 1.001387        exp        1        0 exp(1,0)
3 10000   0.02 1.004672 1.019877        exp        1        0 exp(1,0)
4 10000   0.03 1.027704 1.015408        exp        1        0 exp(1,0)
5 10000   0.04 1.052646 1.047080        exp        1        0 exp(1,0)
6 10000   0.05 1.033982 1.046866        exp        1        0 exp(1,0)

Et maintenant, visualisons le résultat…

ggplot(df,aes(x=lambda, y=response, color=label)) + 
   geom_line() + 
   geom_errorbar(aes(x = lambda, y = response,
                 ymin = response - 2*sd/sqrt(10000), ymax = response + 2*sd/sqrt(10000))) +
   geom_vline(xintercept = 1) + geom_hline(yintercept = 1) + theme_bw()

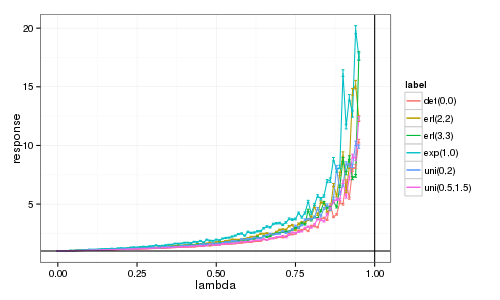
Mmmh. C'est ressemblant mais c'est loin d'être aussi régulier que ce que Jean-Marc montrait. Pourtant, les intervalles de confiance sont effectivement plutôt petits. En regardant son code, il avait en fait exécuté avec N=100,000 et pas N=10,000 comme indiqué dans le texte… (reproducible research, quand tu nous tiens ;) C'est probablement pour cela que j'ai une variance aussi élevée.

Première tentative avec le bon jeu de données

Je vais donc refaire le calcul correspondant vraiment à la figure de Jean-Marc.

df<-experiment(100000)
head(df)

      n lambda response       sd input_type input_p1 input_p2    label
1 1e+00   0.00 1.000000 0.000000        exp        1        0 exp(1,0)
2 1e+05   0.01 1.009352 1.008359        exp        1        0 exp(1,0)
3 1e+05   0.02 1.019517 1.024193        exp        1        0 exp(1,0)
4 1e+05   0.03 1.035593 1.040245        exp        1        0 exp(1,0)
5 1e+05   0.04 1.040472 1.043414        exp        1        0 exp(1,0)
6 1e+05   0.05 1.051982 1.053425        exp        1        0 exp(1,0)

ggplot(df,aes(x=lambda, y=response, color=label)) + 
   geom_line() + 
   geom_errorbar(aes(x = lambda, y = response,
                 ymin = response - 2*sd/sqrt(10000), ymax = response + 2*sd/sqrt(10000))) +
   geom_vline(xintercept = 1) + geom_hline(yintercept = 1) + theme_bw()

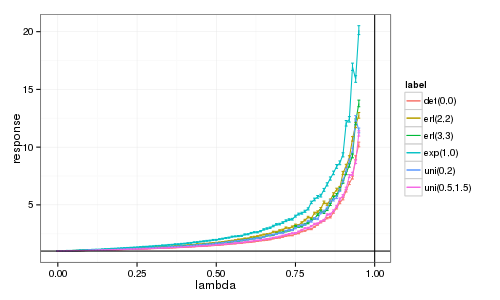
Bon… c'est mieux, plus régulier et les intervalles de confiance sont petits au début mais pas si minuscules quand la charge λ augmente, ce qui est logique. En tous cas, l'utlisation de courbes de Bézier a du tout lisser et c'est pour ça qu'on obtient quelque chose d'un peu moins régulier.

Tentative de "lissage"

Bon, donc dégageons les intervalles de confiance et lissons un peu les choses (normalement, geom_smooth travaille avec les données d'origine et pas directement mean et sd donc ce n'est pas bien propre et ce que ggplot va essayer de faire par défaut puisqu'il y a peu de points, c'est une approximation par un polynôme de degré 2…).

ggplot(df,aes(x=lambda, y=response, color=label)) + 
   geom_point() + 
   geom_errorbar(aes(x = lambda, y = response,
                 ymin = response - 2*sd/sqrt(10000), ymax = response + 2*sd/sqrt(10000))) +

   geom_smooth() + 
   geom_vline(xintercept = 1) + geom_hline(yintercept = 1) + theme_bw()

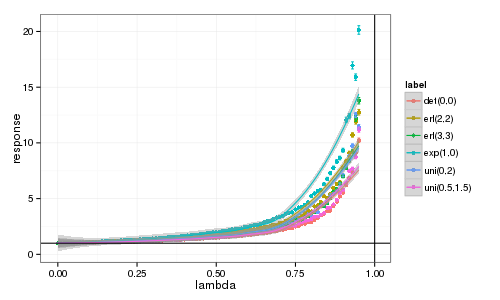
Berk! Bon, je retourne à mes bêtes lignes alors. Je ne sais pas comment interpoler par des courbes de Bézier avec ggplot2. En même temps, est-ce bien raisonnable ? Qu'est-ce que cela veut dire après tout ?…

Version finale avec des labels automatiques

Comme Jean-Marc souhaite appliquer les bonnes pratiques de Jain pour améliorer la lisibilité de son graphique, il déporte les légendes et utilise des flèches pour relier les légendes à leur courbe. Faire ça automatiquement n'est pas très pratique mais voici une tentative.

Commençons par calculer les coordonnées des flèches à partir de df.

labels= sort(unique(df$label))
labels <- data.frame(lambda=0.4+0.05*(1:length(labels)),
                     label=labels)
#labels <- rbind(labels, data.frame(lambda=0.45, label="det(0,0)"))
#labels <- rbind(labels, data.frame(lambda=0.5, label="uni(0,2)"))
#labels <- rbind(labels, data.frame(lambda=0.55, label="uni(0.5,1.5)"))
#labels <- rbind(labels, data.frame(lambda=0.6, label="erl(2,2)"))
#labels <- rbind(labels, data.frame(lambda=0.65, label="erl(3,3)"))

get_resp <- function(df,lambda,label) {
   df[df$lambda==lambda & df$label==label,]$response[1]
}

labels <- ddply(labels, c("lambda","label"), transform,
                response=get_resp(df,lambda,label))
# For some strange reason, one value is messed up. I don't get it but I've lost enough time.
labels[labels$label=="exp(1,0)",]$response=get_resp(df,0.6,"exp(1,0)")

labels$x <- labels$lambda-.25
labels$y <- (round((labels$response + labels$lambda))+
             8*as.numeric(labels$label))/15+1
labels

  lambda        label response    x        y
1   0.45     det(0,0) 1.408300 0.20 1.666667
2   0.50     erl(2,2) 1.735926 0.25 2.200000
3   0.55     erl(3,3) 1.806652 0.30 2.733333
4   0.60     exp(1,0) 2.457051 0.35 3.333333
5   0.65     uni(0,2) 2.207991 0.40 3.866667
6   0.70 uni(0.5,1.5) 2.262871 0.45 4.400000

library(grid) # needed for arrow function
ggplot(df,aes(x=lambda, y=response, color=label)) + theme_bw() +
   geom_line() + 
   geom_point(aes(shape=input_type),size=3,alpha=.4) + 
   geom_vline(xintercept = 1, color="blue") + 
   geom_hline(yintercept = 1, color="blue") +
   geom_text(data=labels, aes(x=x,y=y,label=label),color="black")+
   geom_segment(data=labels, aes(x=x,y=y,xend=lambda,yend=response),
                arrow = arrow(length = unit(0.1,"cm")))+
   scale_color_brewer(palette="Dark2")+
   ylim(0, 6) +
   opts(title= "Temps de réponse moyen en fonction de la charge en entrée") + 
   xlab("Débit normalisé d'entrée (clients/unité de temps)\n(Temps de service = 1 unité de temps)") +
   ylab("Unités de temps")

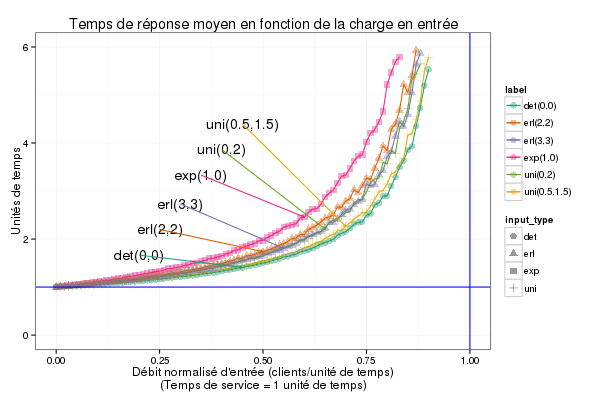
Bon, certaines flèches se croisent mais c'est facile à régler en n'utilisant pas l'ordre des facteurs mais une séquence adaptée. La courbe n'est pas vraiment sympa avec les daltoniens. C'est pour ça que j'ai essayer de varier un peu la forme des points mais il y a probablement un peu trop d'informations sur ce graphe en fait. Évidemment, ça demande un peu plus de travail qu'en retraitant par xfig ou inkscape et ça n'est pas tout à fait aussi beau mais au moins le graphe est reproductible et très facilement extensible… ;)

Le paragraphe qui suit est une retranscription directe du document de Jean-Marc.

Discussion

On remarque au préalable que toutes les courbes sur la figure ont la même forme; au dessus de la droite y=1 qui correspond au temps moyen de service (ce qui est logique car le temps de réponse est égal au temps de service plus un temps d'attente lié à la contention pour l'accès au serveur). Lorsque λ, le débit d'entrée est très faible, il n'y a pas de contention, donc pas d'attente et le temps moyen de réponse est égal au temps moyen de service (=1) et ceci indépendamment de la loi du temps de service. Le système est stable pour λ\<1 et on observe bien la singularité en λ = 1 pour toutes les lois de service (asymptote verticale que l'on devine mais qui est impossible à approcher car les simulations deviennent de plus en plus instables pour les valeurs de λ proches de 1).

On peut également interpréter le temps moyen de réponse par rapport aux aspects aléatoires du système. 1 correspond au temps de réponse s'il n'y avait pas contention. La distance entre la courbe y=1 et la courbe brune (temps de service constant) correspond à la contention liée à la variabilité des arrivées. L'écart entre le courbe brune et les autres correspond à l'impact de la variabilité du temps de service sur le temps de réponse. Ensuite on observe que les courbes sont comparables dans l'ordre de leur variance :

Loi de S	Constant	U_[0.5,1.5]	U_[0,2]	Erl(3,3)	Erl(2,2)	E(1)
Variance	0	1/12	⅓	⅓	½	1

Note: je ne sais pas pourquoi le tableau précédent rend aussi mal une fois exporté en html. Que ça soit avec icedove ou epiphany, les alignements ne sont pas respectés. Avec w3m, c'est nickel par contre… Bref, il doit me manquer une petite configuration.

Les deux courbes confondues (loi U_[0,2] et Erl(3,3)) correspondent à des lois ayant la même variance. On pourrait donc conjecturer que le temps moyen de réponse ne dépend que du débit normalisé d'entrée et de la variance du temps de service. La forme de la loi n'a pas d'importance, seule compte la variance (ce qui est étonnant et qui sera confirmé par la théorie, Formule de Pollatczek-Kintchine.