



précédent: Structures de données élémentaires
monter: UE33/UE43 - Opt1. Algorithmique D.E.U.G. 2ème Année
suivant: À propos de ce document...
Table des matières
Sous-sections
Réponse à l'exercice 1
6
Il suffit de suivre l'évolution des différentes variables:
Elle affecte donc 0 aux variables A,B et C.
Réponse à l'exercice 2
6
Elle affecte 9 à X, Y et Z.
Réponse à l'exercice 3
7
Réponse à l'exercice 4
7
Néanmoins, cela ne marche que parce que les variables sont de type
Entier. Ça ne marcherait pas avec des variables de type Caractère.
Réponse à l'exercice 5
7
Réponse à l'exercice 6
7
Réponse à l'exercice 7
7
Réponse à l'exercice 8
7
Réponse à l'exercice 9
7
Réponse à l'exercice 10
8
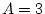 ,
, 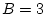 ,
, 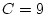
 ,
, 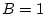 ,
, 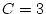
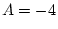 ,
, 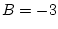 ,
, 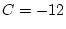
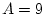 ,
, 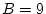 ,
, 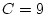
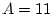 ,
, 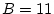 ,
, 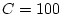
Réponse à l'exercice 11
8
Réponse à l'exercice 12
9
Réponse à l'exercice 13
10
Réponse à l'exercice 14
13
int calcul_somme(int n) {
int i, j, somme = 0;
for (i = 1; i <= n; i++) {
for (j = 1; j <= i; j++) {
somme = somme + i + j;
}
}
return (somme);
}
Réponse à l'exercice 15
13
int calcul_Fibonnacci_iteratif_simple(int n)
{
int tab[100];
int i = 2;
if (n <= 0)
return -1;
tab[0] = 1;
tab[1] = 1;
for (i = 2; i <= n; i++) {
tab[i] = tab[i - 1] + tab[i - 2];
}
return (tab[n]);
}
Réponse à l'exercice 16
13
int calcul_Fibonnacci_iteratif_ruse(int n)
{
int tab[3];
int i = 2;
if (n <= 0)
return -1;
if (n <= 1)
return 1;
tab[2] = 1;
tab[1] = 1;
tab[0] = tab[1] + tab[2];
for (i = 3; i <= n; i++) {
tab[2] = tab[1];
tab[1] = tab[0];
tab[0] = tab[1] + tab[2];
}
return (tab[0]);
}
Réponse à l'exercice 17
13
int calcul_Fibonnacci_recursif(int n)
{
int res = 0;
if (n == 0)
return 1;
if (n == 1)
return 1;
res = calcul_Fibonnacci_recursif(n-1) + calcul_Fibonnacci_recursif(n-2);
return (res);
}
Réponse à l'exercice 18
14
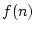 |
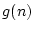 |
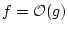 |
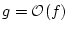 |
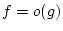 |
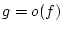 |
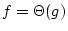 |
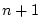 |
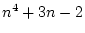 |
Vrai |
Faux |
Faux |
Vrai |
Faux |
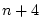 |
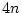 |
Vrai |
Vrai |
Faux |
Faux |
Vrai |
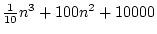 |
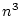 |
Vrai |
Vrai |
Faux |
Faux |
Vrai |
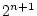 |
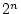 |
Vrai |
Vrai |
Faux |
Faux |
Vrai |
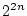 |
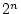 |
Faux |
Vrai |
Vrai |
Faux |
Faux |
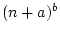 |
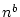 |
Vrai |
Vrai |
Faux |
Faux |
Vrai |
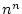 |
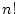 |
Faux |
Vrai |
Vrai |
Faux |
Faux |
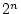 |
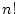 |
Vrai |
Faux |
Faux |
Vrai |
Faux |
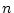 si si
![$ n\equiv0[2]$](img100.png) et 1 sinon et 1 sinon |
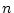 |
Vrai |
Faux |
Faux |
Faux |
Faux |
Réponse à l'exercice 19
17
void affiche_tableau(int *tab, int n) {
int i;
for (i = 0; i < n; i++) {
printf("Tab[%d]=%d\n",i,tab[i])
}
}
Réponse à l'exercice 20
17
void affiche_tableau(int *tab, int n) {
int i;
for (i = 0; i < n; i++) {
printf("Tab[%d]=%d\n",i,tab[i])
}
}
Réponse à l'exercice 21
17
void lire_tableau(int *tab, int n) {
int i;
for (i = 0; i < n; i++) {
printf("Tab[%d]= ?\n",i);
scanf("%d",&(tab[i]));
}
}
Réponse à l'exercice 22
17
Réponse à l'exercice 23
17
Soit
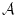 UN algorithme qui résout le problème du MAX. Appliquons
UN algorithme qui résout le problème du MAX. Appliquons
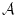 à
à
![$ [t[1]; t[2]; \dots ; t[n]]$](img218.png) , où
, où ![$ t[1]$](img219.png) est le plus grand élément du
tableau. Cet algo renvoie donc
est le plus grand élément du
tableau. Cet algo renvoie donc ![$ t[1]$](img219.png) . On montre par l'absurde que
tout élément qui n'est pas le maximum est comparé au moins une fois
à un élément plus grand que lui : supposons que
. On montre par l'absurde que
tout élément qui n'est pas le maximum est comparé au moins une fois
à un élément plus grand que lui : supposons que ![$ t[2]$](img220.png) ne soit pas
comparé à plus grand que lui. Alors en appliquant
ne soit pas
comparé à plus grand que lui. Alors en appliquant
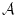 sur l entrée
sur l entrée
![$ [t[1]; t[1] + 1; t[3]; \dots ; t[n]]$](img221.png) , on ne va pas changer le
déroulement précédent de l'algorithme et la réponse retournée est
incorrecte, ce qui contredit l'hypothèse de départ. Comme il y a n-1
éléments qui ne sont pas le maximum, il y a au moins
, on ne va pas changer le
déroulement précédent de l'algorithme et la réponse retournée est
incorrecte, ce qui contredit l'hypothèse de départ. Comme il y a n-1
éléments qui ne sont pas le maximum, il y a au moins 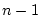 comparaisons.
comparaisons.
Réponse à l'exercice 24
17
Réponse à l'exercice 25
26118
Il est facile de compter le nombre d'opérations nécessaires. À
chaque itération, on démarre à l'élément 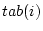 et on le compare
successivement à
et on le compare
successivement à
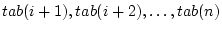 . On fait donc
. On fait donc
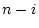 comparaisons. On commence avec
comparaisons. On commence avec 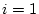 et on finit avec
et on finit avec 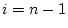 .
Donc on fait
.
Donc on fait
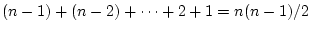 comparaisons, et
comparaisons, et
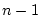 échanges. Le tri par sélection fait donc de l'ordre de
échanges. Le tri par sélection fait donc de l'ordre de 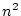 comparaisons.
comparaisons.
void tri_selection_sans_copie(int* tab,int taille){
int i,j,x,ind_min;
for(i=0;i<taille-1;i++){
ind_min=i;
for(j=i+1;j<taille;j++){
if(tab[j]<tab[ind_min]){
ind_min=j;
}
}
x=tab[i];
tab[i]=tab[ind_min];
tab[ind_min]=x;
}
}
Réponse à l'exercice 27
19
On peut compter aussi trés facilement le nombre d'opérations et se
rendre compte qu'il s'agit d'un tri en
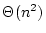 comparaisons et
comparaisons et
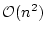 échanges (si par exemple le tableau est donné en ordre
strictement décroissant).
échanges (si par exemple le tableau est donné en ordre
strictement décroissant).
void tri_bulle(int* tab,int taille){
int i,j,x;
for(i=1;i<=taille-1;i++){
for(j=0;j<taille-i;j++){
if(tab[j]>tab[j+1]){
x=tab[j];
tab[j]=tab[j+1];
tab[j+1]=x;
}
}
}
}
Réponse à l'exercice 28
21
Une première méthode peu efficace...
Et une seconde bien plus efficace.
Réponse à l'exercice 29
26
On utilise bien sûr la fonction définie comme ci...
Réponse à l'exercice 30
26




précédent: Structures de données élémentaires
monter: UE33/UE43 - Opt1. Algorithmique D.E.U.G. 2ème Année
suivant: À propos de ce document...
Table des matières
Arnaud Legrand
2003-08-18
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\setboolea...
...=0)}}\hspace{3.5cm}~}
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img186.png)
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\setboolea...
...=0)}}\hspace{3.5cm}~}
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img186.png)
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\setboolea...
...=9)}}\hspace{3.5cm}~}
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img187.png)
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\setboolea...
...est ', \VAR{B})
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img188.png)
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\setboolea...
...est ', \VAR{B})
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img188.png)
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\setboolea...
...est ', \VAR{X})
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img189.png)
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STATE \PC...
... : ', \VAR{HT})
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img190.png)
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STATE \PC...
... B :', \VAR{M})
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img191.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\STAT...
...} ,' Secondes')
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img192.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\STAT...
...} ,' Secondes')
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img193.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
%%
\...
... \ENDIF
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img208.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\STAT...
...st ',\VAR{acc})
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img209.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...xspace
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img62.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...r }}\VAR{somme}
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img210.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
... }}\VAR{tab[n]}
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img211.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
... }}\VAR{tab[0]}
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img212.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...r }}(\VAR{res})
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img213.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...u[i]})
\ENDFOR
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img214.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...u[i]})
\ENDFOR
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img214.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...u[i]})
\ENDFOR
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img215.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...yer }}\VAR{max}
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img216.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...max},\VAR{min})
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img222.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...echange}
\ENDFOR
\END%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img223.png)
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
... \ENDFOR
\ENDFOR
\END%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img231.png)
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\te...
...AR{L}))
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img234.png)
![\begin{boxedminipage}{9.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\te...
... \ENDIF
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img235.png)
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\te...
... \ENDIF
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img236.png)
![\begin{boxedminipage}{10.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\t...
...{L_2}))
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img237.png)
![\begin{boxedminipage}{10.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\t...
...de()}))
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img238.png)
![\begin{boxedminipage}{11cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\tex...
...Liste\_Vide()})
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img239.png)
![\begin{boxedminipage}{12cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\tex...
... \ENDIF
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img240.png)
![\begin{boxedminipage}{9.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\te...
...L_2})))
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img241.png)
![\begin{boxedminipage}{10.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\t...
... \ENDIF
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img242.png)
![\begin{boxedminipage}{10.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\t...
...A.fd}))
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img243.png)
![\begin{boxedminipage}{15cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\tex...
...A.fd}))
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img244.png)
![\begin{boxedminipage}{15cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\tex...
....fd})))
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img245.png)
![\begin{boxedminipage}{15cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\tex...
...{L}))))
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img246.png)
![\begin{boxedminipage}{15cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\tex...
...fd}))))
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img247.png)