



précédent: Quelques exercices
monter: UE33/UE43 - Opt1. Algorithmique D.E.U.G. 2ème Année
suivant: Calcul du maximum et du minimum
Table des matières
Sous-sections
Analyser un algorithme revient à prévoir les ressources (i.e. la
quantité de mémoire) nécessaires à cet algorithme et à mesurer son
temps d'exécution. En général, quand on analyse plusieurs algorithmes
candidats pour un problème donné, on arrive aisément à identifier le
candidat le plus efficace. Ce type d'analyse peut révéler plusieurs
candidats valables et permet d'éliminer les autres.
L'analyse d'un algorithme, même simple, peut s'avérer difficile. Il
est donc nécessaire de se donner des outils mathématiques pour
parvenir à nos fins.
Les fonctions que l'on considère dans cette section sont des fonctions
de
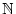 dans
dans
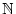 . Soient
. Soient 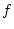 et
et 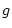 deux fonctions.
deux fonctions.
Définition 1
On dira que
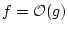
si et seulement si il existe
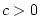
et
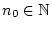
tel que
Définition 2
On dira que
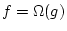
si et seulement si il existe
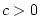
et
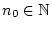
tel que
Définition 3
On dira que
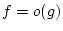
si et seulement si
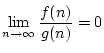
.
Définition 4
On dira que
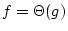
si et seulement si
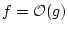
et
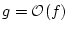
.
On remarquera que
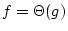
si et seulement si
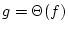
.
Remarque 1
Comme on ne manipule que des fonctions de
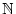
dans
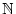
et que l'on
s'intéresse uniquement à leur comportement à l'infini, on pourra
sommer les
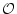
et les
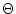
sans risque.
L'utilisation de la notation
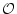 permet de majorer le comportement
d'une fonction et la notation
permet de majorer le comportement
d'une fonction et la notation 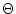 permet d'éviter d'avoir une
majoration trop grossière. La notation
permet d'éviter d'avoir une
majoration trop grossière. La notation 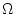 signifie qu'une
fonction croit au moins aussi vite qu'un autre.
signifie qu'une
fonction croit au moins aussi vite qu'un autre.
Ces notations permettent donc de comparer deux fonctions. On pourra
faire l'analogie suivante avec la comparaison sur des nombres réels:
Le temps d'exécution d'un algorithme sur une entrée particulière est
le nombre d'opération élémentaires exécutées. Reprenons un à un les
algorithmes de la section 3.1 et évaluons leur
complexité
Pour le moment, nous dirons que chaque ligne de notre pseudo-code
demande une quantité de temps constante. L'execution de la ligne 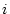 prendra donc un temps
prendra donc un temps 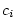 . Dans l'étude qui va suivre, le temps
d'exécution va évoluer d'une formulation brouillonne utilisant tous
les coûts des
. Dans l'étude qui va suivre, le temps
d'exécution va évoluer d'une formulation brouillonne utilisant tous
les coûts des 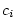 , vers une formulation beaucoup plus simple, plus
concise et plus facile à manipuler.
, vers une formulation beaucoup plus simple, plus
concise et plus facile à manipuler.
Le coût de l'exécution de l'algorithme dépend donc de n. On a
donc
Le temps d'exécution de cet algorithme est donc 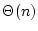 . On
remarquera que l'on utilise un tableau de taille
. On
remarquera que l'on utilise un tableau de taille 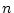 et une variable
de boucle. L'occupation mémoire est donc
et une variable
de boucle. L'occupation mémoire est donc 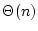 .
.
Le temps d'exécution de cet algorithme est donc encore 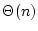 .
Par contre, on n'utilise qu'un tableau de taille 3 et une variable de
boucle. L'occupation mémoire est donc
.
Par contre, on n'utilise qu'un tableau de taille 3 et une variable de
boucle. L'occupation mémoire est donc 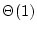 , ce qui est bien
meilleur.
, ce qui est bien
meilleur.
Récursif
On a donc
Il est parfaitement possible d'obtenir une forme close pour 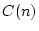 mais nous nous contenterons pour l'instant d'un encadrement.
mais nous nous contenterons pour l'instant d'un encadrement.
Donc
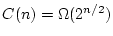 . De même, on a
. De même, on a
On a donc
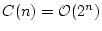
L'évaluation de l'occupation mémoire est un peu différente. Un arbre
d'appel permet de se convaincre aisément qu'il est en 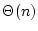 . Le
temps d'exécution de l'algorithme est de l'ordre du nombre de noeuds
de l'arbre d'appel alors que l'occupation mémoire est de l'ordre de la
hauteur de l'arbre.
. Le
temps d'exécution de l'algorithme est de l'ordre du nombre de noeuds
de l'arbre d'appel alors que l'occupation mémoire est de l'ordre de la
hauteur de l'arbre.




précédent: Quelques exercices
monter: UE33/UE43 - Opt1. Algorithmique D.E.U.G. 2ème Année
suivant: Calcul du maximum et du minimum
Table des matières
Arnaud Legrand
2003-08-18
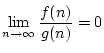 .
.![]() permet de majorer le comportement
d'une fonction et la notation
permet de majorer le comportement
d'une fonction et la notation ![]() permet d'éviter d'avoir une
majoration trop grossière. La notation
permet d'éviter d'avoir une
majoration trop grossière. La notation ![]() signifie qu'une
fonction croit au moins aussi vite qu'un autre.
signifie qu'une
fonction croit au moins aussi vite qu'un autre.
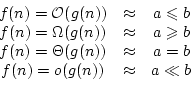
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...pace{1cm}\null
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](algo1.jpg)
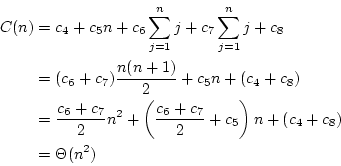
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...pace{1cm}\null
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](algo2.jpg)
![]() . On
remarquera que l'on utilise un tableau de taille
. On
remarquera que l'on utilise un tableau de taille ![]() et une variable
de boucle. L'occupation mémoire est donc
et une variable
de boucle. L'occupation mémoire est donc ![]() .
.
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...pace{1cm}\null
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](algo3.jpg)
![]() .
Par contre, on n'utilise qu'un tableau de taille 3 et une variable de
boucle. L'occupation mémoire est donc
.
Par contre, on n'utilise qu'un tableau de taille 3 et une variable de
boucle. L'occupation mémoire est donc ![]() , ce qui est bien
meilleur.
, ce qui est bien
meilleur.
![\begin{boxedminipage}{.9\linewidth}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC...
...pace{1cm}\null
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](algo4.jpg)
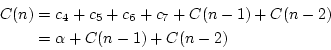
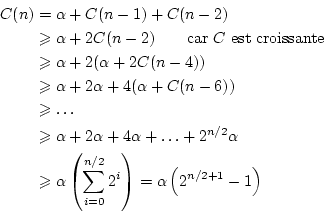
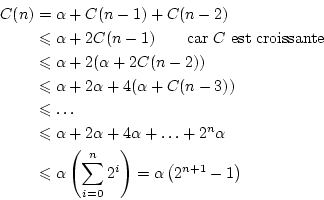
![]() . Le
temps d'exécution de l'algorithme est de l'ordre du nombre de noeuds
de l'arbre d'appel alors que l'occupation mémoire est de l'ordre de la
hauteur de l'arbre.
. Le
temps d'exécution de l'algorithme est de l'ordre du nombre de noeuds
de l'arbre d'appel alors que l'occupation mémoire est de l'ordre de la
hauteur de l'arbre.