Calcul du maximum et du minimum

Exercice 19   Écrire un algorithme Écrire_Tableau(tableau,taille) qui affiche à l'écran les différentes valeurs d'un tableau tableau de taille taille. Voir réponse 19. Traduisez votre algorithme en langage C. Voir réponse 19.

Exercice 20   Écrire un algorithme Écrire_Tableau(tableau,taille) qui affiche à l'écran les différentes valeurs d'un tableau tableau de taille taille. Voir réponse 20. Traduisez votre algorithme en langage C. Voir réponse 20.

Exercice 21   Écrire un algorithme Lire_Tableau(tableau,taille) qui lit taille élément au clavier et les affecte dans les différentes cellules du tableau tableau. Voir réponse 21. Traduisez votre algorithme en langage C. Voir réponse 21.

Les algorithmes que nous allons écrire dans cette section n'utilisent que des affectations et des comparaisons. Il n'y pas besoin d'effectuer des opérations arithmétiques et c'est le nombre de comparaison que nous allons évaluer pour chacun des algorithmes que nous allons proposer.

Calcul du maximum

Algorithme

Exercice 22   Écrire une fonction Maxi_Tableau qui prend en entrée un tableau d'entier et sa taille et renvoie un entier qui est la valeur du plus grand élément du tableau. Voir réponse 22.

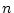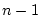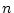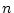Une analyse rapide montre que, pour un tableau de taille $n$, on effectue exactement $n-1$ comparaisons et, au plus, $n$ affectations. Dans quel cas effectue-t-on $n$ affectations ? Dans quel cas, n'en effectue-t-on qu'une ? Cet algorithme est optimal en ce qui concerne le nombre de comparaisons.

Exercice 23   Démontrer l'optimalité de l'algorithme précédent. Voir réponse 23.

Calcul du maximum et du minimum

Exercice 24   Proposez un algorithme naïf permettant de calculer à la fois le minimum et le maximum d'un tableau. Voir réponse 24.

Algorithme rusé

L'idée pour améliorer l'algorithme est de regrouper les éléments à comparer par paires, i.e. de comparer à chaque tour de boucle $t[2k]$ et $t[2k+1]$, et ensuite comparer un seul des deux à min_tmp (lequel ?), et l'autre à max_tmp. Dans la suite, on distinguera bien les cas où la longueur du tableau est paire des cas où elle est impaire.

Exercice 25   Écrire un algorithme un peu plus rusé et effectuant moins de comparaisons.

Montrer que le nombre de comparaison est 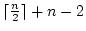$\lceil \frac{n}{2}\rceil + n - 2$. On peut montrer que cet algorithme est optimal mais celà sort du cadre de ce cours.