Comme nous l'avons vu en section 1.2, une variable est
un espace mémoire nommé, de taille fixée. Il est donc possible de
parler de l'adresse d'une variable (notée &var en C et que
nous noterons ![]() var dans ce cours). L'adresse d'une variable
étant une valeur, elle a donc un type : c'est un pointeur. On
distingue un pointeur sur un Entier, d'un pointeur sur un Caractère, d'un
pointeur sur un Réel, même si ce sont tous des adresses. Le type du
pointeur est nécessaire pour pouvoir le déréférencer, c'est à dire
accéder à la valeur pointée par le pointeur (si add est un
pointeur, la valeur pointée par add est notée *add en
C et nous la noterons
var dans ce cours). L'adresse d'une variable
étant une valeur, elle a donc un type : c'est un pointeur. On
distingue un pointeur sur un Entier, d'un pointeur sur un Caractère, d'un
pointeur sur un Réel, même si ce sont tous des adresses. Le type du
pointeur est nécessaire pour pouvoir le déréférencer, c'est à dire
accéder à la valeur pointée par le pointeur (si add est un
pointeur, la valeur pointée par add est notée *add en
C et nous la noterons ![]() add
add![]() dans ce cours). Un pointeur
particulier est le pointeur NIL (NULL en C). Il représente
une adresse inaccessible et c'est donc une valeur que l'on utilise
pour dire que le pointeur n'a pas de valeur déterminée. Il est
primordial de toujours initialiser ses pointeurs à la valeur NIL.
Cela permet de détecter plus simplement les déréférencement de
pointeurs non initialisés...On remarquera qu'un tableau peut être
représenté par un pointeur (l'emplacement de son premier élément en
mémoire) et un entier (sa taille).
dans ce cours). Un pointeur
particulier est le pointeur NIL (NULL en C). Il représente
une adresse inaccessible et c'est donc une valeur que l'on utilise
pour dire que le pointeur n'a pas de valeur déterminée. Il est
primordial de toujours initialiser ses pointeurs à la valeur NIL.
Cela permet de détecter plus simplement les déréférencement de
pointeurs non initialisés...On remarquera qu'un tableau peut être
représenté par un pointeur (l'emplacement de son premier élément en
mémoire) et un entier (sa taille).
Enfin, une structure (ou enregistrement) est un produit nommé de
plusieurs types. Définissons un nouveau type
![]()
ainsi qu'une variable ind de ce type.
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STRUCT{{\...
...u}}}\xspace \VAR{ind}
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img154.png)
Il est ensuite aisé d'accéder aux différents champs de cette structure de la façon suivante:
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STATE \VA...
...gin} \GETS ''bspear''
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img155.png)
En C, les tableaux, les pointeurs et les structures sont des structures de données de base (elles sont fournies par le langage). Nous allons maintenant voir un certain nombre d'autres structures de données qui n'existent pas au départ dans le langage C, mais que l'on peut construire assez aisément.
Bien sûr, cette linéarité est purement virtuelle. À la différence du tableau, les éléments n'ont aucune raison d'êtres contigus ni ordonnés en mémoire.

La façon dont on met en ![]() uvre ces structures dépend des langages
même si la façon dont cela est présenté ici ressemble fortement à
celle du langage C. Une façon simple de se représenter une liste,
consiste à se dire qu'une liste
uvre ces structures dépend des langages
même si la façon dont cela est présenté ici ressemble fortement à
celle du langage C. Une façon simple de se représenter une liste,
consiste à se dire qu'une liste ![]() est soit vide
est soit vide ![]() , soit
constituée d'une tête
, soit
constituée d'une tête ![]() (qui est donc la valeur du premier élément
de la liste) et d'une queue
(qui est donc la valeur du premier élément
de la liste) et d'une queue ![]() (qui est le reste de la liste).
(qui est le reste de la liste).
La manipulation d'une liste peut donc se faire grâce aux fonctions suivante:
La liste que nous avons donné en exemple peut donc se définir par:
En terme de pointeurs et de structures, une liste d'entier peut se représenter grâce au type suivant:
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STRUCT{{\...
...{suivant}
\ENDSTRUCT
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img166.png)
La liste que nous avons donné en exemple pourrait se définir par:
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STATE {\t...
...AR{NIL}\xspace
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img167.png)
Pour conclure, retenons simplement qu'il est possible d'accéder en temps constant à la tête de la liste.
Écrire une fonction qui renvoie le
![]() élément d'une liste:
Voir réponse 28.
élément d'une liste:
Voir réponse 28.
Écrire une fonction qui indique si un élément appartient à une liste: Voir réponse 28.
Écrire une fonction qui concatène deux listes: Voir réponse 28.
Écrire une fonction qui renverse une liste: Voir réponse 28.
Écrire une fonction qui insère un élément dans une liste triée: Voir réponse 28.
Écrire une fonction qui fusionne deux listes triées: Voir réponse 28.
Pour vous entrainer, vous pourrez évaluer la complexité en mémoire et en temps de chacune de ces fonctions et les réécrire de façons itérative.
L'opération d'insertion dans une pile est généralement appelée
Empiler. L'opération de suppression est souvent appelée
Dépiler. Nous allons mettre en ![]() uvre la structure de pile
à l'aide d'un tableau.
uvre la structure de pile
à l'aide d'un tableau.
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STRUCT{{\...
...met+1]}
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img169.png)
Cependant, dans cette mise en ![]() uvre, comme on inclue notre pile
dans un tableau, la taille de la pile est bornée. On peut s'affranchir
de cette limitation en utilisant une simple liste chaînée. En effet,
empiler un élément consiste simplement à rajouter un maillon, dépiler
un élément consiste à en enlever un et à ce que la pile soit
représentée par la queue de la liste précédente, tester si la pile est
vide consiste à regarder s'il y a un maillon. Le type utilisé pourrait
alors ressembler à ceci:
uvre, comme on inclue notre pile
dans un tableau, la taille de la pile est bornée. On peut s'affranchir
de cette limitation en utilisant une simple liste chaînée. En effet,
empiler un élément consiste simplement à rajouter un maillon, dépiler
un élément consiste à en enlever un et à ce que la pile soit
représentée par la queue de la liste précédente, tester si la pile est
vide consiste à regarder s'il y a un maillon. Le type utilisé pourrait
alors ressembler à ceci:
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STRUCT{{\...
...VAR{tete}
\ENDSTRUCT
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img170.png)
On peut alors écrire les fonctions précédentes très simplement:
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\FUNC[{\te...
...t_pile}
\ENDIF
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img171.png)
Bien sûr, cette linéarité est purement virtuelle. Tout comme pour la liste chaînée, les éléments n'ont aucune raison d'êtres contigus ni ordonnés en mémoire.

En terme de pointeurs et de structures, ce type peut donc se définir de la façon suivante.
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STRUCT{Ma...
...recedant}
\ENDSTRUCT
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img174.png)
La liste que nous avons donné en exemple pourrait se définir par
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STATE Mai...
...${\VAR{cell3}}}
\END
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img175.png)
L'opération d'insertion dans une pile est généralement appelée
Enfiler. L'opération de suppression est souvent appelée
Défiler. Cette structure peut, comme pour une pile, se mettre
en ![]() uvre avec un tableau mais elle souffrira des même limitations
que pour la pile. Le plus simple consiste à utiliser une liste
doublement chaînée:
uvre avec un tableau mais elle souffrira des même limitations
que pour la pile. Le plus simple consiste à utiliser une liste
doublement chaînée:
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STRUCT{Ma...
...\VAR{fin}
\ENDSTRUCT
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img176.png)
Une file où auraient été enfilées successivement les valeurs 12, 25, 4 et 7 se représenterait donc ainsi :
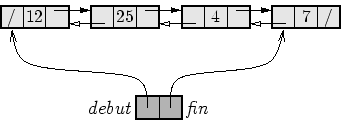
Bien sûr, une fois de plus, cette linéarité est purement virtuelle:

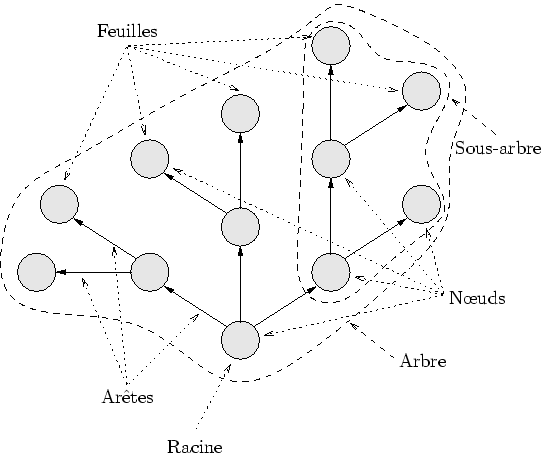
Un arbre est un ensemble de n![]() uds (appelés aussi parfois sommets)
reliés par des arêtes tel que chaque n
uds (appelés aussi parfois sommets)
reliés par des arêtes tel que chaque n![]() ud (à part la racine qui en
a 0) ait exactement une arête pointant vers lui. La racine est donc un
n
ud (à part la racine qui en
a 0) ait exactement une arête pointant vers lui. La racine est donc un
n![]() ud particulier puisqu'il n'a pas de prédécesseur. Les feuilles
sont les noeuds sans sucesseurs.
ud particulier puisqu'il n'a pas de prédécesseur. Les feuilles
sont les noeuds sans sucesseurs.
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STRUCT{No...
...tbf{Noeud}}}\xspace }
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img180.png)
Encore une fois, cette organisation est purement virtuelle. L'arbre suivant
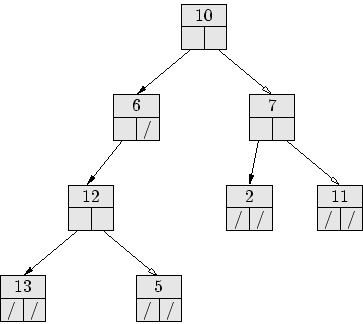

Voir réponse 29.
Écrire une fonction qui calcule le nombre de n![]() uds d'un arbre donné.
Voir réponse 29.
uds d'un arbre donné.
Voir réponse 29.
Écrire une fonction qui calcule la somme des valeurs des n![]() uds
d'un arbre donné.
Voir réponse 29.
uds
d'un arbre donné.
Voir réponse 29.
Écrire une fonction qui calcule la plus grande des valeurs des n![]() uds
d'un arbre donné.
Voir réponse 29.
uds
d'un arbre donné.
Voir réponse 29.
On suppose disposer du contructeur
![]()
qui, étant donné un entier val et deux arbres gauche et
droit, construit un arbre dont la racine est étiquetée par
val et dont le fils droit est droit et le fils gauche
gauche. Ce constructeur, en association avec l'![]()
, permet de construire n'importe quel
arbre binaire.
Évidemment, ce n'est pas la seule façon de transformer une liste en arbre. On aurait également pu mettre les valeur sur la gauche de l'arbre. L'idéal (pour l'équilibrage de l'arbre) étant de mettre à chaque étape la moitié de la liste à gauche et l'autre moitié à droite...
On peut également écrire simplement une fonction qui transforme un arbre en liste.
Voir réponse 30.
![\begin{boxedminipage}{8.5cm}%
\begin{algorithmic}[1]%
\begin{sf}
\STRUCT{No...
...fils[n]}
\ENDSTRUCT
%
\end{sf} \end{algorithmic}%
\end{boxedminipage}%
\par](img185.png)
Quand il n'est pas possible de borner le degré de l'arbre, il suffit d'utiliser une des structures dynamiques que nous avons vu en début de section (liste, file, ...).