RICM4: Évaluation de Performance 2019

Table of Contents

Sitemap

---> misc
| ---> 2016
| ---> 2015
| ---> 2014
| ---> 2013
| ---> 2012
`--> Agenda

Informations Générales

Le pad du cours est ici: http://pads.univ-grenoble-alpes.fr/p/INFO4_EP_19

Le planning avec les salles de cours est disponible ici.

La page de l'an dernier est ici.

Programme du cours prévisionnel

Semaine Cours (Jeudi, 8h00 en 035) TD (Vendredi, 11:30)
16-17 janvier [AL] Introduction au cours et aux files d'attente et Simulation d'une M/M/1 [JA] Simulation à évènement discret d'une M/M/1
23-24 janvier [JA] Modélisation des files d'attente et des systèmes Markoviens. Pas de TD
30-31 janvier [AL] Chaînes de Markov à Temps Discret Rappel sur les valeurs propres. [JA] Page Rank + présentation du DM
6-7 février Chaînes de Markov à Temps Discret: LRU, M/M/1 aux instants de sauts [JA] [JA] Études de petits systèmes Markovien et d'un cache Web (correction et code R)
13-14 février [AL] Analyse des logs d'un serveur Web (data) et Introduction au Processus de Poisson [JA] Poursuite de l'analyse des logs et propriétés du processus de Poisson (interarrivé, uniformité,…). Autres références avec les preuves (Cours Geneviève Gauthier , cours Étienne Pardoux)
20-21 février [AL/JA?] Processus de Poisson [JA] Aloha!
28-1 mars Vacances Vacances
5-6 mars [AL] Chaîne de Markov à temps continu [AL] Processus de naissance et de mort, file M/M/1, TD sur les iles d'attente. En bonus, un aide mémoire sur la M/M/1 et sur la M/M/K/K.
12-13 mars [AL] Quick [JA] Correction du Quick
19-20 mars [AL] Régression linéaire [JA] La M/M/1 avec rejet
26-27 mars [AL] La régression linéaire en pratique [JA] Réseaux de Jackson
2 avril Pas de cours [JA] Révisions
6 avril Examen le lundi 6 avril à 8h00  

Retour sur le DM et le TD

Nom Quick DM
Sacha GUYOT A+ A-
Thomas FRION C B+
Luís Filipe VELASCO DA SILVA A+ E
Alan GUIVARCH B+ A
Raphaël AUDIN B B
Adrien ARTAUD A+ B+
Gaëtan RIVAL B- B+
Romain PASDELOUP B A-
Alexandre SALMON B B+
Killian PAREILLEUX A- A
Robin DELBOS B- A-
Dima ASSI   A-
Houda EL AJI B B+
LOMBARD Myriam A B+
Idriss SAJIDE B- B+

TDs

Simulation à évènement discrets de file d'attentes

L'objectif du TD est de comprendre la bonne façon d'organiser une simulation à évènement discret (sans reposer trop intensément sur les hypothèse type arrivées de Poisson) avec la notion d'état du système, d'évènements possible et de mise à jour de l'état du système. Si vous lisiez des bouquins qui expliquent comment faire de la simulation à évènement discret, il n'est pas clair que ça vous aiderait vraiment. Le mieux est d'en écrire un ensemble pour que vous compreniez comment procéder. Pour celà, on va s'intéresser au cas simple d'une file d'attente.

Direction, le pad du cours: http://pads.univ-grenoble-alpes.fr/p/INFO4_EP_19

Modélisation et principe de simulation

  • Paramètres du système
    • Taux d'arrivée dans le système lambda (en tâches par seconde)
    • Taux de service du système mu (en tâches par seconde)
    • Politique de service (on va coder FIFO là mais on essaye de coder tout ça de la façon la plus générique possible)

  • Description des variables d'état importantes:

    • Date courante t
    • Dates d'arrivées Arrival: dates calculées à partir d'inter-arrivées (input)
    • Temps de service Service: temps générés (input)
    • Temps résiduel Remaining: initialisé à NA, passe à Service quand un job arrive dans le système et décroit alors vers 0.
    • Date de terminaison Completion: initialisé à NA, passe à la date courante t lorsque Remaining passe à 0.
    • Client actuellement servi CurrClient (utile pour caractériser la politique de service utilisée): initialisé à NA

    J'ai finalement rajouté une variable NextArrival qui permet d'éviter des contortions ou des notations un peu lourdes. Cette variable est initialisée à 1 et sera incrémentée jusqu'à dépasser le nombre de tâches total.

  • Évolution possible
    • Soit une arrivée
    • Soit la terminaison d'une tâche

  • Structure du code: 

    while(T) {
    dtA = ...  # temps jusqu'à la prochaine arrivée
    dtC = ...  # temps jusqu'à la prochaine terminaison
    if(is.na(dtA) & is.na(dtC)) {break;}
    dt = min(dtA,dtC)
    # Mettre à jour comme il faut.
}

Objectif de la séance:

  • Avoir une version correcte de cette simulation
  • Structurer ce code obtenir une data-frame avec tout ce qu'il faut pour étudier le temps de réponse en fonction du taux d'arrivée:

  • Fixer le taux de service mu à 1 et étudier (je veux une courbe!) le temps de réponse en fonction du taux d'arrivée lambda. Idéalement, vous devriez obtenir quelque chose du genre: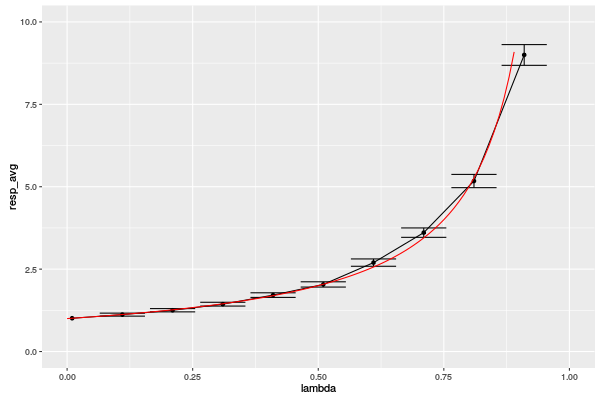

    MM1.png

Bibliographie