RICM4: Évaluation de Performance
Table of Contents
Sitemap
Informations Générales
Jean-Marc Vincent est chargé des cours et Arnaud Legrand s'occupe des TDs.
Le planning avec les salles de cours est disponible sur ADE.
La page de l'an dernier est ici.
Programme du cours
| Semaine | Cours (Jeudi, 8h00, salle 035 en général) | TD (Vendredi, 11:30, F107 ou exceptionnellement 8:00 en F112 |
|---|---|---|
| 14-15 janvier | Intro (JMV) | Mesures de performance de code (AL) |
| 21-22 janvier | Test statistique | 8h00 Mesures de performance de code (AL) |
| 28-29 janvier | Régression linéaire | Journée Neige. Have fun! *<B) |
| 4-5 février | Début de chaînes de Markov | Régression linéaire en pratique |
| 11-12 février | Fin des chaînes de Markov | Cache et chaines de Markov |
| 18-19 février | reporté au 2 mars: Processus de Poisson | reporté au 11 mars |
| 25-26 février | Vacances universitaires | Vacances universitaires |
| 3-4 mars | Aloha | 8h00 Random walks and Page ranking |
| 10-11 mars | 8h00 et 11h30 : Simulation de files d'attentes | |
| 17-18 mars | Files d'attente M/M. Calcul des propriétés. Processus de Markov en temps continu. Un chapitre sur le sujet à toute fin utile. | Files d'attente. En bonus, un aide mémoire sur la M/M/1. |
| 24-25 mars | Réseaux de files d'attentes | Présentation et réflexion sur la tâche finale: DM2 |
| 31 mars- 1 avril | Pas de cours | Pas de TD, reporté au mardi 5 |
| mardi 5 avril | 8h00 Open bar, révision examens |
DM
DM1: Mesures de performance d'un code parallèle
Ce travail au fil de l'eau s'est fait sur plusieurs séances et consistait à améliorer le plan d'expérience et l'analyse d'un code parallèle simple (voir la section "Mesures de performance").
Voici les liens vers les documents des étudiants:
- Cenyo Medewou: Très bien dans l'ensemble.
- Il manque les infos sur la compilation et les options de compilation dans les premières expériences.
- Dans l'expérience 2: non, ça n'augmente pas "exponentiellement". Arrêtez de voir des exponentielles partout!
- À propos de l'experiment 3, ce n'est pas parceque dans ce cas précis la randomisation de l'ordre n'a rien changé que tu ne veux pas l'utiliser. C'est ce qui permet de t'assurer de ne pas te faire avoir par un paramètre externe non maîtrisé. Mais c'était bien de tester pour vous rendre compte de ce l'impact de la randomisation. La conclusion c'est il n'y a pas d'impact visible sur les performances donc je l'active pour éviter des problèmes de mesures.
- Pour l'expérience 4, il est très surprenant que l'option de compilation ait eu un effet sur built-in.
- En conclusion, vous avez fait une étude assez propre, de type "One
Factor At a Time" (vous avez étudié l'impact de
thread_level, puis de la taille du tableau, puis de la randomisation, puis des options de compilation). C'est assez classique mais en fait c'est "mal" et il y a moyen de mieux faire. Je ne vous en ai pas vraiment parlé en cours car l'analyse est un peu plus déroutante quand on n'a pas l'habitude. N'hésitez pas à venir me voir si vous voulez que je vous raconte.
- Florian Popek: Très bien. Quelques infos manquantes ou difficiles à trouver: compilation et options de compilation (built-in semble meilleur que sequential, as tu activé les optimisations?), le lien direct vers les scripts plutôt qu'un inline (plus simple en org-mode), la régression est faite sur les moyennes et pas sur les mesures d'origine, ce qui te fait perdre une partie de l'information sur la variabilité. Tu devrais utiliser des chemins relatifs plutôt qu'absolus dans tes scrips et ne pas t'en remettre à bash pour contrôler les valeurs des paramètres à tester.
- Yacine Ndiaye: Ouh là, c'est très confus, en particulier la
partie 4. Pour la partie 2, effectivement, en
-O0, la version parallèle fini par être meilleur que la version séquentielle mais en-03, ce n'est même pas la peine, la version séquentielle est trop rapide et il faudrait probablement aller chercher des tailles de tableaux bien plus élevées. Dommage que tu ne l'ai pas dit plus clairement. Pour la partie 3, tu as bien vu qu'il valait mieux unthread_levelpas trop élevé. Tu aurais pu remarquer que sur tes expériences il fallait même qu'il soit le plus petit possible et essayer du coup d'encore plus petites valeurs… - Rémi Gattaz: Super. Attention, tu as un lien cassé "Running this
created the following output" dans la section "Experiment 3 : Thread
levels". Dans la partie régression linéaire, il aurait probablement
été intéressant de mettre les trois data-frames ensemble et de faire
un facet car les échelles des 3 graphes sont proches mais pas
identiques. Au final ta version parallèle s'en sors très bien. Je me
trompe ou tu es resté en
-O0?… Au final, avec tes régressions, il me semble que tu pouvais répondre assez bien à la question initiale i.e., "À partir de quelle taille de tableau devient-il opportun d’utiliser la version parallèle?" - Abdelaziz Founas: Le rapport est sur rpubs. Euh.. Ton rapport est propre et tout mais il me semble que tu n'as absolument pas amélioré le plan d'expérience proposé. Tu n'as absolument pas discuté l'impact de certains des paramètres discutés en TD (optimisation, thread_level, …). D'autre part, conclure qu'activer la version parallèle à partir de 250,000 en se basant sur le fait que tes lignes se croisent là, c'est très très foireux. C'est justement ce que je ne voulais pas que vous fassiez.
- Quentin Faure : OK, tu voulais jouer avec docker. Pourquoi pas ? Il y a des données, des courbes mais où sont vraiment les analyses/conclusions ? C'est un peu rapide. "In parallel execution mode, the Docker execution looks slower than the native one". Il n'en a pas que l'air. C'est clairement bien plus lent sur tes courbes. De l'ordre de grandeur de si on avait eu une exécution séquentielle en fait…
- Tanguy Mathieu: ça ne va pas bien loin là… Tu abuses.
- Marwan Hallal: où est l'analyse ?
- Damien Crastes: les modifications que tu apportes ne sont pas claires dans ton rapport ("le code à était augmenté afin de permettre la selection facile du nombre de threads" par exemple mais je ne sais pas quel nombre de threads tu as utilisé… au final dans ta data-frame, je n'ai une information que sur Size et Type). D'autre part, tu as tendance à conclure de façon très hâtive sans réel arguments (par exemple "Vu que [..] la réponse la plus logique à cette question serait que le temps de commnication entre les threads compense le gain possible de performances." Euuuuh…). Le nombre de threads a effectivement une influence forte (mais pour le lire sur tes courbes, il faut être motivé parcequ'elles piquent les yeux). Enfin, quand tu dis "Sur une machine plus performante que la mienne, il pourrait être possible de tester de manière précise les limites de chacun des algorithmes […]", penses-tu vraiment que c'est une machine plus performante qu'il te faut ou bien plutôt un protocole expérimental et une analyse plus propre? :) Perso, je suis incapable de quantifier quoi que ce soit avec les courbes que tu donnes.
DM2
Ce travail s'appuie sur les deux séances de TD sur la simulation à évènements discrets de files d'attentes. Le DM est à rendre (github, rpubs, mail, …) pour le 27 avril.
On utilisera des arrivées exponentielles de paramètre λ mais des temps de service distribués selon la loi Gamma \(Γ(k, \mu)\).
- Lorsque le paramètre de forme \(k\) est un entier, la loi Gamma
correspond à une distribution d’Erlang, c’est à dire à la somme
de \(k\) variables aléatoires indépendantes de même loi exponentielle
de paramètre d’échelle \(\mu\). Les paramètres \(k\) et \(\mu\) permettent
donc de jouer sur l’espérance et la variance de la loi. Ainsi
rgamma(N,shape=1,rate=mu)équivaut àrexp(N,mu). Enfin, l'espérance d'une \(Γ(k, \mu)\) vaut \(k/\mu\) et la variance vaut \(k/\mu^2\). En jouant sur \(k\) on peut donc obtenir une loi avec l'espérance souhaitée et une variance arbitrairement grande (\(k>1\)) ou petite (\(k<1\)).
Vous vous assurerez que le temps de service de votre file d'attente est d'espérance \(1/\mu\) (avec \(\mu=1\) pour normaliser) et que vous savez contrôler sa variance.
- Nota Bene:
Ce point n'étant visiblement pas clair pour tout le monde, je vous invite à lire ceci: https://en.wikipedia.org/wiki/Gamma_distribution
L'espérance d'une Gamma(shape,scale) est \(shape*scale\) et sa variance est \(shape*scale^2\).
Donc, si on souhaite que le taux de service soit constant et égal à 1, il faut prendre \(scale=1/shape\) auquel cas la variance vaut \(1/shape\). Du coup:
N=100000 shape = 1 x=rgamma(n=N,shape=shape,scale=1/shape) mean(x) sd(x)[1] 0.9978392 [1] 0.9972472
shape = 10 x=rgamma(n=N,shape=shape,scale=1/shape) mean(x) sd(x)[1] 1.001646 [1] 0.3152573
shape = .1 x=rgamma(n=N,shape=shape,scale=1/shape) mean(x) sd(x)[1] 1.009283 [1] 3.213299
- Lorsque le paramètre de forme \(k\) est un entier, la loi Gamma
correspond à une distribution d’Erlang, c’est à dire à la somme
de \(k\) variables aléatoires indépendantes de même loi exponentielle
de paramètre d’échelle \(\mu\). Les paramètres \(k\) et \(\mu\) permettent
donc de jouer sur l’espérance et la variance de la loi. Ainsi
- Vous modifierez votre code pour étudier les performances d'une file
implémentant les politiques suivantes:
- FIFO (déjà fait)
- LIFO
- LIFO avec préemption (i.e., si une nouvelle tâche arrive la tâche en cours est suspendue, remise en attente et terminée plus tard)
- SRPT: (Shortest Remaining Processing Time First), c'est à dire qui exécute en priorité la tâche pour laquelle il reste le moins de travail à effectuer. Cette politique est donc clairvoyante (i.e., elle connaît la durée des tâches et tire parti de cette information pour les ordonnancer) et préemptive, ce qui lui donne a priori un avantage par rapport aux autres politiques
- Vous étudierez l'impact du taux d'arrivée, de la variance du temps de service et de la politique de la file sur le temps de réponse. Vous prendrez soin de concevoir un plan d'expérience adapté et de représenter l'incertitude dans vos analyses. Vous tenterez d'expliquer vos résultats.
Vous avez le droit de lire mes corrigés des années précédentes si ça peut vous aider. Ce qui m'importe, c'est que vous ne pompiez pas bêtement (je m'en rendrai compte), que vous ne fassiez pas les bourrins (l'argument "c'était trop long, ça prenait des plombes à calculer" n'est pas recevable, si ça vous arrive, c'est que votre plan d'expérience est mal conçu ou votre code vraiment trop mal écrit ;) ) et que vous mettiez bien en oeuvre tout ce dont on a pu parler pendant ce semestre.
Commentaires:
- Abdelaziz Founas:
- Pourquoi caches-tu ton code ? Il y a des fois où ça serait utile pour le relecteur.
- Mettre 1/(1-x) comme référence, c'est bien.
- Pourquoi 1, 10, 100 en shape ? 1 correspondant à une loi exponentielle, tester .1 plutôt que 100 aurait été plus intéressant… Mais au moins, contrairement à pas mal d'autres, tu as fait varier ce qu'il fallait.
- Tu fournis plein de graphes. Il faut que tu les regroupes lorsque tu fais tes analyses afin que le lecteur puisse suivre le fil de ta pensée et comparer (avec la même échelle et tout) les différentes figures.
- "Pour conclure", tes conclusions ne vont pas plus loin que "c'est plus haut, c'est plus bas, ça se ressemble"… Constater, c'est bien mais j'aurais voulu que tu cherches à comprendre et que tu expliques ce qu'il se passe.
- Rémi Gattaz: Wow, du ".org". ;)
- Attention, quand tu te rapproches de la zone d'instabilité, évaluer les performances est de plus en plus compliqué. Pour voir la différence entre les différentes politiques, il n'est pas clair que ça soit le meilleur endroit où se placer…
- Oh là, très très bizarre de faire varier mu! Pourquoi n'as tu pas tout simplement refais l'analyse de la 1.4.1 avec une variance de temps de service faible, puis avec une variance de temps de service élevée ? J'ai beaucoup de mal à interpréter ce qu'il se passe. Par contre ta conclusion est exacte.
- Ndiaye Yacine:
- Ouh là, c'est histoire de shape et de scale, ça t'a posé problème visiblement. Dommage que tu n'aies pas demandé à tes collègues ou à moi-même…
- Au final en 3.1, tu fixes shape et scale à 1 donc tu es sur une loi exponentielle. Du coup, à part SRPT qui est meilleure, les autres sont équivalentes.
- Et en 3.2, j'ai plus de mal à comprendre ce que tu fais (et je
pense que toi aussi).
lifo_preemptionetsrptsont différentes mais pourquoi ?…
- Florian Popek:
- Beeeeerk! Bonjour le copier/coller pour les différentes politiques! Si tu codes toujours comme ça, je ne sais pas si je vais te prendre en stage!
- "LIFO semble être en deuxième position devant FIFO et PLIFO (ces deux derniers ne peuvent pas être départagés)." C'est étrange. Là, tu as un shape de 1 donc une loi exponentielle et elles sont toutes trois équivalentes…
- "Faire varier mu" ? Mais qu'est ce que vous avez tous avec ça ? Ça n'a pas de sens. C'est la variance qu'il faut varier, pas l'espérance. Si tu changes mu, tu ne peux plus mettre 1/(1-x) dans tes graphes. Et pour m>1, ça devient carrément n'imp…
- Pareil que d'autres, j'ai droit à du "machin conserve sa place de leader" ou du "truc est en deuxième position" mais c'est pas un commentaire sportif que je vous demande. Constater, c'est bien mais je veux que vous m'expliquiez ce qu'il se passe.
- Quentin Faure:
- Tu injectes une charge d'entrée de 0 à 3 alors que ton taux de service est de 1. En d'autres termes, alors que ton serveur est capable de traiter en moyenne une tâche par seconde, tu lui en balances jusqu'à trois pas seconde… Forcément, c'est complètement instable et les valeurs que tu calcules n'ont plus aucun sens… :(
- D'autre part, tu n'as pas fait varier la variance du temps de service.
- Cenyo Medewou:
- Argh, tes courbes ne ressemblent à rien (en tous cas pas à l'habituelle forme 1/(1-x)). Les valeurs en y sont bien trop élevées, ton système est saturé. Mais pourquoi donc as-tu fixé mu à 0.25 et injecté une charge entre 0 et 1 ??? C'est comme Quentin, ça n'a aucun sens. Et comme lui, tu n'a pas fait varier la variance du temps de service comme je le demandais.
- Par contre, au moins, tu essayes d'expliquer ce qu'il se passe et ça c'est vraiment bien.
- Tanguy Mathieu:
- Euh… tu as une drôle de façon d'étudier ça. On voulait voir l'influence du taux d'arrivée et de la variance du taux de service.
- Marwan Hallal:
- Pareil que Tanguy. Tu abuses.
- Damien Crastes:
- Ce qui est bien là, c'est que tu essayes d'expliquer ce que tu observes (par exemple "les taches “rapides” voleront les places d’éxéction des taches lentes")
- Une représentation graphique des tableaux de valeurs pour res* dans la section "test de masse par modèle", ça aurait été plus que bienvenu…
- Mais varier ainsi mu avec lambda fixé arbitrairement à .7, ça n'a aucun sens… Au fait, tu t'es rendu compte que ton Ts ne variait pas du tout comme tu pensais et ne correspondait pas à mu ?…
TDs
Mesures de performance
- Forkez le repos suivant: https://github.com/alegrand/M2R-ParallelQuicksort
- Puis faites un checkout sur votre machine. Ce repository comporte un code C qui réalise un quicksort séquentiel ou multi-threadé.
- On souhaite évaluer l'opportunité de remplacer l'implémentation du
quicksort de la libc par une version parallèle afin que toutes les
applications puissent bénéficier automatiquement des architectures
multi-coeurs. L'objectif de ces séances est de répondre aux
questions suivantes:
- Quels sont les paramètres sur lesquels on peut jouer simplement pour améliorer les performances de ces différentes versions ?
- À partir de quelle taille de tableau devient-il opportun d'utiliser la version parallèle ?
Modélisation et Simulation d'un Cache Web
On dispose de \(N=100\) objets et on va étudier les performances d'un cache LRU de taille \(K\). Pour simplifier, on va supposer qu'un des objets est plus populaire (probabilité \(a\)) que les autres (probabilité \(b\)).
N = 100 a = 0.1 b = (1-a)/(N-1) K = 20 T = 1000 sequence = sample(1:N,T,replace=T,prob=c(a,rep(b,N-1)))
Alors, à quoi cela ressemble-t-il ?
head(sequence, n=50)
[1] 24 73 12 70 38 57 92 5 69 18 1 77 37 94 48 43 76 90 4 28 68 52 91 81 94 [26] 61 56 27 18 11 19 45 64 54 77 28 13 73 20 10 18 83 18 85 80 82 64 97 50 73
Est-ce que la séquence a bien l'air aléatoire ?
plot(sequence)
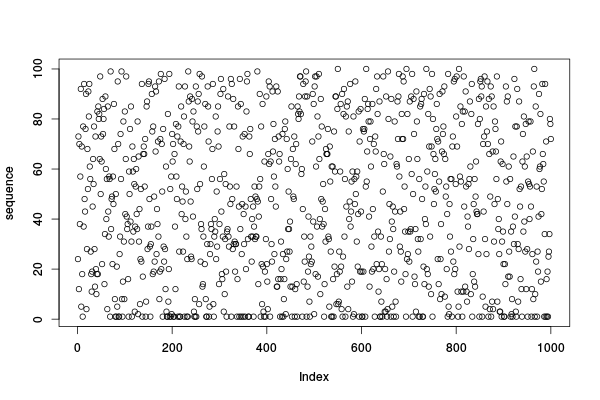
Est-ce que c'est bien distribué comme ça devrait
hist(sequence,breaks=100)
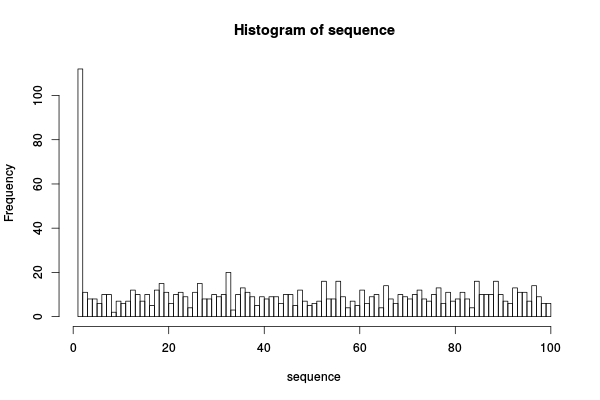
Maintenant, simulons LRU.
cache=rep(NA,K); # cache vide à l'origine. miss=c(); # pour compter les défauts de caches missA=c(); # pour compter les défauts de caches de A posA=c(); # position de l'objet A for(v in sequence) { if(v %in% cache) { where = (1:K)[cache==v]; if(where!=1) { if(where==K) { cache = c(v,cache[1:(where-1)]); # attention, les () sont obligatoires dans les ranges (":"). } else { cache = c(v,cache[1:(where-1)],cache[(where+1):(length(cache))]); } } miss=c(miss,0); } else { cache = c(v,cache[1:(length(cache)-1)]); miss=c(miss,1); if(v==1) { missA=c(missA,1); } else { missA=c(missA,0); } } if(1 %in% cache) { posA = c(posA,((1:K)[!is.na(cache) & cache==1])); } else { posA = c(posA,NA); } }
Alors, quand a-t-on des défauts de cache ? Forcément les premiers sont tous des défauts de caches…
head(miss, 100)
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 0 1 [38] 1 1 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 1 1 1 [75] 0 1 1 1 1 0 1 0 1 1 1 1 0 0 1 0 1 0 0 0 0 1 1 1 0 1
head(missA, 100)
[1] 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [38] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 [75] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
plot(miss)
Regardons où se balade notre objet A.
plot(posA); lines(posA);
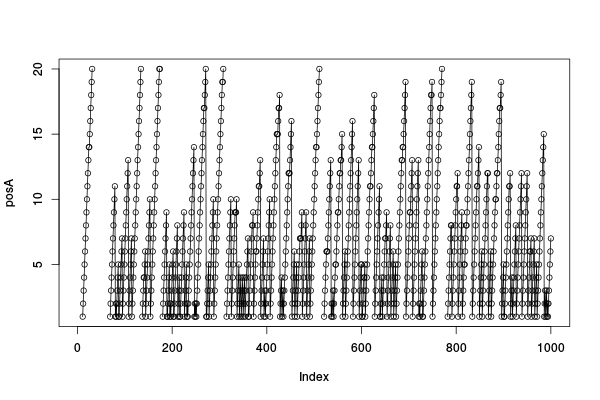
Alors, quelle est la probabilité de défaut de cache ?
err = sd(miss)/sqrt(length(miss)); mean(miss)-2*err; mean(miss)+2*err;
[1] 0.69881 [1] 0.75519
Bon, pas terrible finalement comme intervalle de confiance. En plus, on voit bien qu'au début on est à cache froid et que les premiers accès pourraient avoir un impact fort sur ce qui suit et "biaiser la trajectoire". De plus, le fait qu'on ait un défaut de cache à un moment n'est pas vraiment indépendant du fait qu'on vienne d'avoir un défaut de cache. Peut-on vraiment appliquer le théorème centrale limite pour calcule un intervalle de confiance dans ces conditions? Il faudra certainement calculer des trajectoires bien plus longues pour être sûr. Les chaînes de Markov permettent de calculer ces probabilités de façon exacte.
options(width=160) M=matrix(rep(0,N*N),nrow=N); for(i in 1:N) { M[i,i] = (i-1)*b; M[i,1] = a; if(i<N) M[i,i+1] = 1-sum(M[i,]); # et oui,... c'est quand même plus simple comme formule ;) } options(digits=3); # Restreignons nous à 3 digits M[1:20,1:20]; # Début de la matrice M[(N-19):N,(N-19):N]; # Fin de la matrice
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
[1,] 0.1 0.90000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[2,] 0.1 0.00909 0.8909 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[3,] 0.1 0.00000 0.0182 0.8818 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[4,] 0.1 0.00000 0.0000 0.0273 0.8727 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[5,] 0.1 0.00000 0.0000 0.0000 0.0364 0.8636 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[6,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0455 0.8545 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[7,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0545 0.8455 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[8,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0636 0.8364 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[9,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0727 0.8273 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[10,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0818 0.8182 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[11,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0909 0.809 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[12,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.100 0.800 0.000 0.000 0.000 0.000 0.000 0.000 0.000
[13,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.109 0.791 0.000 0.000 0.000 0.000 0.000 0.000
[14,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.118 0.782 0.000 0.000 0.000 0.000 0.000
[15,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.127 0.773 0.000 0.000 0.000 0.000
[16,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.136 0.764 0.000 0.000 0.000
[17,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.145 0.755 0.000 0.000
[18,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.155 0.745 0.000
[19,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.164 0.736
[20,] 0.1 0.00000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.173
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
[1,] 0.727 0.173 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[2,] 0.000 0.736 0.164 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[3,] 0.000 0.000 0.745 0.155 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[4,] 0.000 0.000 0.000 0.755 0.145 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[5,] 0.000 0.000 0.000 0.000 0.764 0.136 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[6,] 0.000 0.000 0.000 0.000 0.000 0.773 0.127 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[7,] 0.000 0.000 0.000 0.000 0.000 0.000 0.782 0.118 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[8,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.791 0.109 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[9,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.800 0.100 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[10,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.809 0.0909 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[11,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.8182 0.0818 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[12,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.8273 0.0727 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[13,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.8364 0.0636 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000
[14,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.8455 0.0545 0.0000 0.0000 0.0000 0.0000 0.00000
[15,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.8545 0.0455 0.0000 0.0000 0.0000 0.00000
[16,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.8636 0.0364 0.0000 0.0000 0.00000
[17,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.8727 0.0273 0.0000 0.00000
[18,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.8818 0.0182 0.00000
[19,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.8909 0.00909
[20,] 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.90000
Alors, on cherche \(\pi\) tel que \(\pi.M=\pi\). Mais du coup, ce sont les vecteurs propres de \({}^tM\) que l'on cherche (les valeurs propres sont les mêmes mais pas les vecteurs propres…):
E=head(eigen(t(M))) head(E$values)
[1] 1.000+0i 0.891+0i 0.882+0i 0.873+0i 0.864+0i 0.855+0i
OK, c'est la première, qui vaut 1, qui nous intéresse. Prenons le vecteur associé:
ssp=E$vectors[,1];
ssp = Re(ssp/(sum(ssp)))
options(digits=7);
ssp
[1] 1.000000e-01 9.082569e-02 8.241590e-02 7.471348e-02 6.766504e-02 6.122075e-02 5.533414e-02 4.996189e-02 4.506367e-02 4.060192e-02 3.654173e-02 [12] 3.285064e-02 2.949854e-02 2.645745e-02 2.370147e-02 2.120658e-02 1.895056e-02 1.691286e-02 1.507451e-02 1.341797e-02 1.192708e-02 1.058696e-02 [23] 9.383897e-03 8.305289e-03 7.339557e-03 6.476080e-03 5.705118e-03 5.017754e-03 4.405833e-03 3.861903e-03 3.379165e-03 2.951423e-03 2.573035e-03 [34] 2.238875e-03 1.944286e-03 1.685048e-03 1.457339e-03 1.257703e-03 1.083022e-03 9.304839e-04 7.975577e-04 6.819696e-04 5.816799e-04 4.948620e-04 [45] 4.198829e-04 3.552856e-04 2.997722e-04 2.521893e-04 2.115136e-04 1.768393e-04 1.473660e-04 1.223887e-04 1.012872e-04 8.351755e-05 6.860370e-05 [56] 5.613030e-05 4.573580e-05 3.710640e-05 2.997056e-05 2.409398e-05 1.927518e-05 1.534147e-05 1.214533e-05 9.561218e-06 7.482693e-06 5.819872e-06 [67] 4.497174e-06 3.451319e-06 2.629577e-06 1.988217e-06 1.491162e-06 1.108813e-06 8.170202e-07 5.962039e-07 4.305917e-07 3.075655e-07 2.171051e-07 [78] 1.513157e-07 1.040295e-07 7.047160e-08 4.698107e-08 3.078070e-08 1.978759e-08 1.245885e-08 7.666988e-09 4.600192e-09 2.683446e-09 1.516730e-09 [89] 8.273072e-10 4.333518e-10 2.166756e-10 1.026356e-10 4.561623e-11 1.878284e-11 7.043726e-12 2.347859e-12 6.708259e-13 1.548047e-13 2.580091e-14 [100] 2.345533e-15
Comme on pouvait s'y attendre, la première coordonnée de \(\pi\) (ssp dans
notre code) est égale à a. C'est bon, vous voyez pourquoi ?
Alors que peut-on faire une fois qu'on a ce fameux vecteur ? Par exemple calculer la probabilité que A soit dans le cache:
sum(ssp[1:K])
[1] 0.9024148
Tout à l'heure, on a compté dans missA chaque fois qu'on ramenait A
dans le cache.
errA = sd(missA)/sqrt(length(missA)); mean(missA); mean(missA) - 2*errA; mean(missA) + 2*errA; sum(ssp[(K+1):N]*a); # somme sur les cas où A est à l'extérieur du cache et qu'on le demande...
[1] 0.009628611 [1] 0.002380204 [1] 0.01687702 [1] 0.009758522
On a bien encadré la bonne valeur mais c'est pas terrible comme encadrement. Pour être sûr, juste du 0.009, il aurait fallu simuler plus de pas de temps:
(sd(missA)/.5E-3)**2
[1] 38196.14
Et comment calcule-t-on à partir de ça la probabilité de défaut de cache tout court ?
err = sd(miss)/sqrt(length(miss)); mean(miss) mean(miss)-2*err; mean(miss)+2*err; sum(ssp[1:K])*(1-(a+(K-1)*b)) + sum(ssp[(K+1):N])*(1-(K*b)) # la valeur exacte!
[1] 0.727 [1] 0.69881 [1] 0.75519 [1] 0.7361441
Cool, du coup, cerise sur le gâteau, voici la probabilité de défaut de cache en fonction de la taille du cache:
pmiss=c(); for(K in 1:N) { pmiss[K] = sum(ssp[1:K])*(1-(a+(K-1)*b)) + sum(ssp[(K+1):N])*(1-(K*b)) # la valeur exacte! } library(ggplot2) ggplot(data=data.frame(size=(1:N),pmiss=pmiss), aes(x=size,y=pmiss)) + geom_point() + theme_bw() + xlab("Taille du cache") + ylab("Probabilité de défaut de cache")
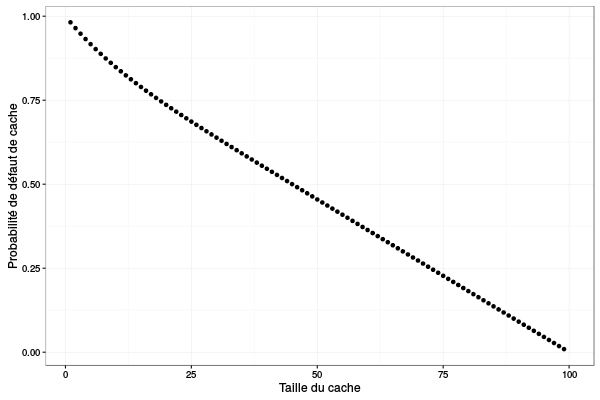
Bon, on voit donc bien là l'intérêt de passer par une chaîne de Markov plutôt que par une simulation à évènement discret pour un système aussi simple. On remarque également la simplicité de cette "courbe" qui est quasi linéaire. Quand \(N\) est grand, il y a certainement moyen d'avoir carrément une formule…
Pour vous entraîner:
- Étudiez de la même façon la politique "Move-Ahead" vue en cours et comparez à "Move-to-front/LRU" en fonction de la taille du cache.
- Construisez une chaîne de Markov adaptée (donc bien plus petite) à la taille du cache et retrouvez les probabilités précédentes.
- Construisez la chaîne de Markov dans le cas où il y a deux objets \(A\) très populaires.
- Faites une simulation à évènement discret en supposant cette fois-ci que la popularité des objets suit une loi de puissance (i.e., \(P(i)\) proportionnel à \(\alpha^i\) avec \(\alpha \in ]0,1[\) ).
La conclusion que vous devriez tirer de tout cela est que ces modèles, même très grossiers, vous donnent les bonnes tendances
TD marches aléatoires
- Google: notion de popularité, pas basée uniquement sur le contenu qui est facilement "forgeable" mais plutôt sur les interconnexions entre les pages.
Intuitivement:
- plus on pointe vers la page i, plus elle est populaire. Donc la popularité est proportionnelle au degré entrant.
- plus le degré sortant d'une page est élevé, plus sa contribution à la popularité des pages devrait être faible
- Plus une page est populaire, plus sa contribution à la popularité des autres pages est élevée (notion "d'expert").
Au final il semble y avoir un point compliqué, la définition de la popularité est récursive à cause du 3ème point. Une équation possible serait:
\(\pi_i = \sum_{j} 1/|\sum_k L_{j,k}| \pi_j\) si \(L\) est la matrice des connexions avec des 0 et des 1
La popularité d'une page, c'est défini par la fréquence à la quelle les gens cliquent vers cette page, ce que Google va avoir du mal à tracer complètement… Et intuitivement, les surfeurs, se baladent sur le graphe du web. Quels sont les problèmes potentiels
- Revenir plusieurs fois sur la même page. Dans le cadre d'une exploration aléatoire, ça n'est pas forcément un problème.
- D'où part on ? Est-ce grave ? Il pourrait y avoir plusieurs composantes connexes et notre surfer serait bloqué juste dans une. S'il n'y a que quelques composantes, pourquoi pas, notre marche aléatoire pourrait nous donner des stats intéressantes mais si c'est plus fragmenté, ça va être compliqué.
- Si on a une page sans lien vers d'autres pages, c'est un puits et tout surfeur va fatalement y tomber et y rester coincé.
Il faudrait considérer que le graphe est fortement connexe mais ce n'est pas le cas. Une solution envisagée par les fondateurs de Google, était de se "téléporter". En moyenne au bout de 5 clicks, on repart au hasard de n'importe où. Ça revient à rajouter des probas très faibles vers tout le monde.
Au final, tout ça revient au même. Calculer des statistiques sur une marche aléatoire dans le graphe ou bien calculer la distributation stationnaire de la chaine de Markov associée (c'est à dire les valeurs/vecteurs propres de la distribution associée), c'est pareil.
Après discussions, on identifie 3 méthodes pour calculer le régime stationnaire:
- Faire une marche aléatoire sur le graphe associé et on calcule des statistiques à la fin sur la fréquence de passage dans chaque page. Intuitivement, la complexité est très très faible mais on a une estimation d'assez mauvaise qualité.
- Calculer les valeurs propres de la matrice associée (comme on a fait plus haut pour le cache). C'est très coûteux (\(n^3\)) pour un graphe de la taille du web mais on a un calcul exact
Itérer la fonction! C'est à dire partir d'un vecteur \(\pi=(1/N,1/N,\dots,1/N)\).
Que se passe-t-il sur la matrice ? Si \(A= MDM^{-1}\) alors \(A^k = MD^kM^{-1}\). Vu que notre matrice a une seule valeur propre à 1 et que les autres sont plus petites que 1, elles vont disparaître lors de l'itération et il ne restera plus que celle associée au vecteur propre 1.
Pour la prochaine fois: tester ces différentes méthodes sur: une ligne, un anneau, et une sucette. Vous pouvez regarder ici pour voir comment faire pour générer ces graphes.
Enfin, deux documents que vous pouvez vouloir regarder et dont je me suis inspiré pour cette séance: cette série de slides (lien d'origine) et cet article publié dans CACM en 2011 mais dont voici la version mise à jour et libre d'accès sur arxiv.
TD simulation à évènements discrets de files d'attentes
- Description du système
- λ: taux d'arrivée (task/s) mais en fait il y a une loi d'arrivée
- μ: taux de service (task/s) mais en fait il y a une loi de service
- politique de service: FIFO, LIFO, avec préemption, sans préemption, ….
- Variables
- N: le nombre de tâches
- t_in : arrivée dans le système [tableau de réels], trié
- next_arrival: [entier]
- t_out: sortie du système [tableau de réels]
- t_s: temps de service [tableau de réels]
- t_r: temps de traitement restant [tableau de réels]
- Waiting: [tableau d'entiers]
- Running: [entier] peut être NA
- t: la date courrante [réel]
- Transition
- Option 1: arrivée d'une tâche
- Option 2: fin de la tâche courante
- Calculer dt: dans combien de temps arrive le prochain évènement
- Mettre à jour
- update_running: t_r car c'est potentiellement ce qu'on utilise pour décider quelle sera la prochaine tâche à exécuter
- push_task (si une tâche est arrivée):
- met à jour Waiting
- run_task
- run_task:
- mettre à jour Waiting (pop)
- mettre à jour Running
Attention pour pouvoir faire des effets de bord à l'extérieur de
l'environnement courant, il faut utiliser l'opérateur
<<-. Illustration
X=1:5 f = function() { X[2] = -1 } g = function() { X[2]<<- -1 } X; f(); X g(); X
[1] 1 2 3 4 5 [1] 1 2 3 4 5 [1] 1 -1 3 4 5
Allons-y!
set.seed(42) simulate = function(N = 5, lambda = .7, mu = 1, type="exp") { t_in = cumsum(rexp(N,lambda)); next_arrival = 1; t_s = switch(type, exp = rexp(N,mu), det = rep(times=N, 1/mu), unif = runif(N,min=.5/mu,max=1.5/mu)); t_r = t_s; t_out = rep(NA,times=N); running = NA; waiting = c(); t = 0; update_running = function() { if(!is.na(running)) { t_r[running] <<- t_r[running] - dt if(t_r[running] <=0) { t_out[running] <<- t running <<- NA } } } push_task = function() { # if policy = fifo.... waiting <<- c(waiting,next_arrival); if(!is.na(next_arrival) & (next_arrival<N)) { next_arrival <<- next_arrival + 1 } else { next_arrival <<- NA } } run_task = function() { # if policy = fifo.... ## print(running); if(!is.na(running)) { ## print("WAAAT?!?"); return ; } else { ## print("No running task, let's pick a new one"); if(length(waiting)>0) { running <<- waiting[1]; waiting <<- waiting[-1]; } } } while(T) { ## print("#######"); ## print(t_in); ## print(t_s); ## print(t_r); ## print(t_out); # computing dt dt1 = NA dt2 = NA if(!is.na(next_arrival)) { dt1 = t_in[next_arrival] - t} if(!is.na(running)) { dt2 = t_r[running] } if (is.na(dt1) & is.na(dt2)) { break; } dt = min(c(dt1,dt2),na.rm=T) ## print(dt); t = t + dt; update_running(); if(!(is.na(next_arrival)) & (t_in[next_arrival]==t)) { push_task(); } run_task(); ## print(running); } data.frame(t_in=t_in, t_s=t_s, t_out=t_out) } simulate()
t_in t_s t_out
1 0.2833383 1.4636271 1.746965
2 1.2274744 0.3139846 2.060950
3 1.6324616 0.4101296 2.471080
4 1.6870214 1.1915978 3.662677
5 2.3629880 0.7148625 4.377540
Warning messages:
1: In if (!(is.na(next_arrival)) & (t_in[next_arrival] == t)) { :
la condition a une longueur > 1 et seul le premier élément est utilisé
2: In if (!(is.na(next_arrival)) & (t_in[next_arrival] == t)) { :
la condition a une longueur > 1 et seul le premier élément est utilisé
3: In if (!(is.na(next_arrival)) & (t_in[next_arrival] == t)) { :
la condition a une longueur > 1 et seul le premier élément est utilisé
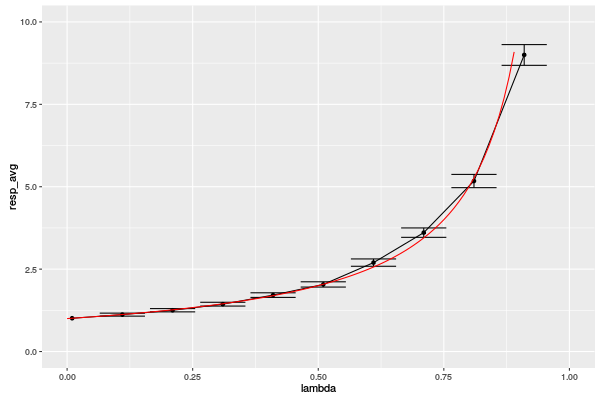
res=data.frame(); for(lambda in c(seq(from=.01, to = .99, by = .1))) { df = simulate(N=10000,lambda=lambda); t_resp = df$t_out - df$t_in; res = rbind(res, data.frame(lambda=lambda, resp_avg = mean(t_resp), resp_err = 2*sd(t_resp)/sqrt(length(t_resp)))); } res
There were 41 warnings (use warnings() to see them) lambda resp_avg resp_err 1 0.01 1.009810 0.02025290 2 0.11 1.120074 0.02251617 3 0.21 1.252510 0.02486425 4 0.31 1.437145 0.02839750 5 0.41 1.712342 0.03443981 6 0.51 2.036360 0.03970012 7 0.61 2.697728 0.05574192 8 0.71 3.607823 0.07125421 9 0.81 5.173664 0.10038978 10 0.91 8.998469 0.15717782
library(ggplot2); myrate = function(x) {1/(1-x)} ggplot(res,aes(x=lambda,y=resp_avg)) + geom_point() + geom_line() + geom_errorbar(aes(ymin=resp_avg-2*resp_err, ymax=resp_avg+2*resp_err)) + xlim(0,1) + ylim(0,10) + stat_function(fun = myrate, geom = "line",color="red")