[W8] - The global convergence time of stochastic gradient descent in non-convex landscapes: Sharp estimates via large deviations
W. Azizian, F. Iutzeler, J. Malick, and P. Mertikopoulos. Working paper.
Abstract
In this paper, we examine the time it takes for stochastic gradient descent (SGD) to reach the global minimum of a general, non-convex loss function. We approach this question through the lens of randomly perturbed dynamical systems and large deviations theory, and we provide a tight characterization of the global convergence time of SGD via matching upper and lower bounds. These bounds are dominated by the most “costly” set of obstacles that the algorithm may need to overcome to reach a global minimizer from a given initialization, coupling in this way the global geometry of the underlying loss landscape with the statistics of the noise entering the process. Finally, motivated by applications to the training of deep neural networks, we also provide a series of refinements and extensions of our analysis for loss functions with shallow local minima.
arXiv link: https://arxiv.org/abs/2503.16398
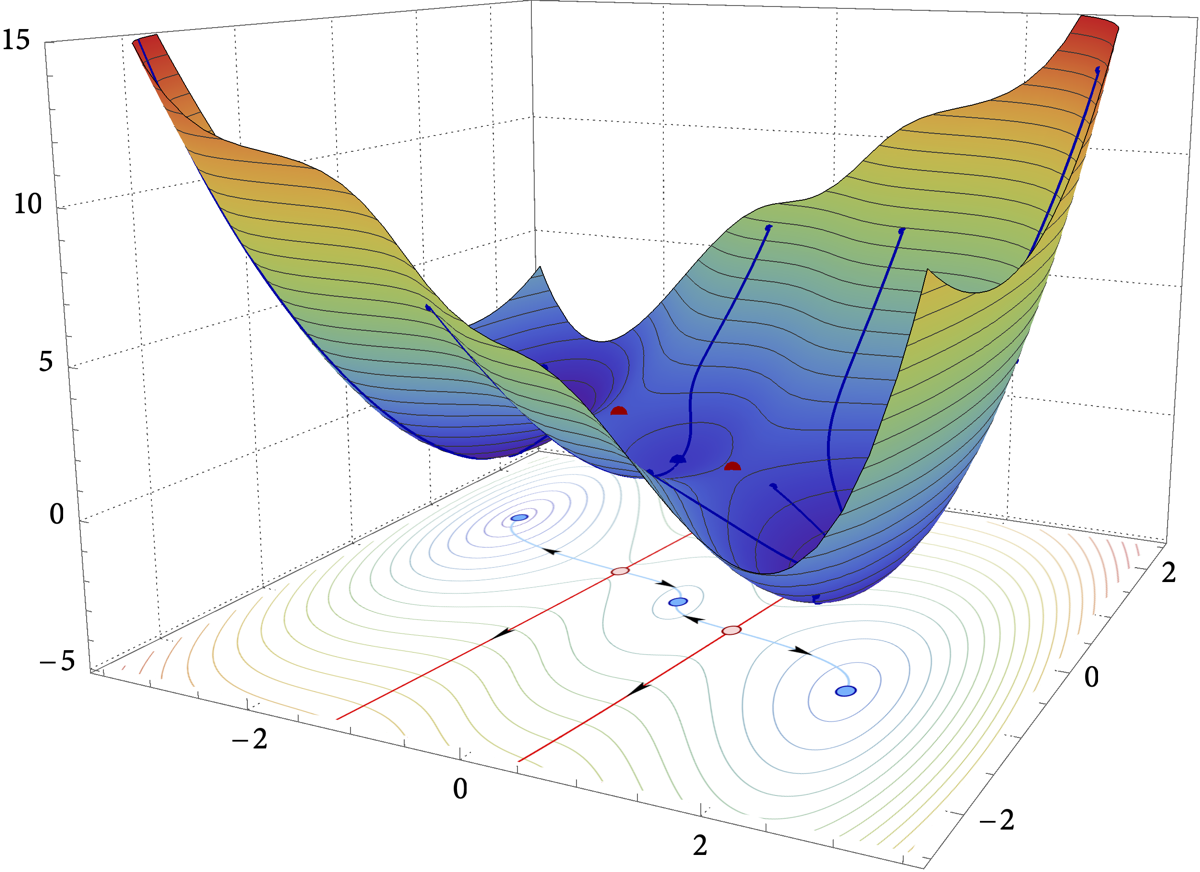
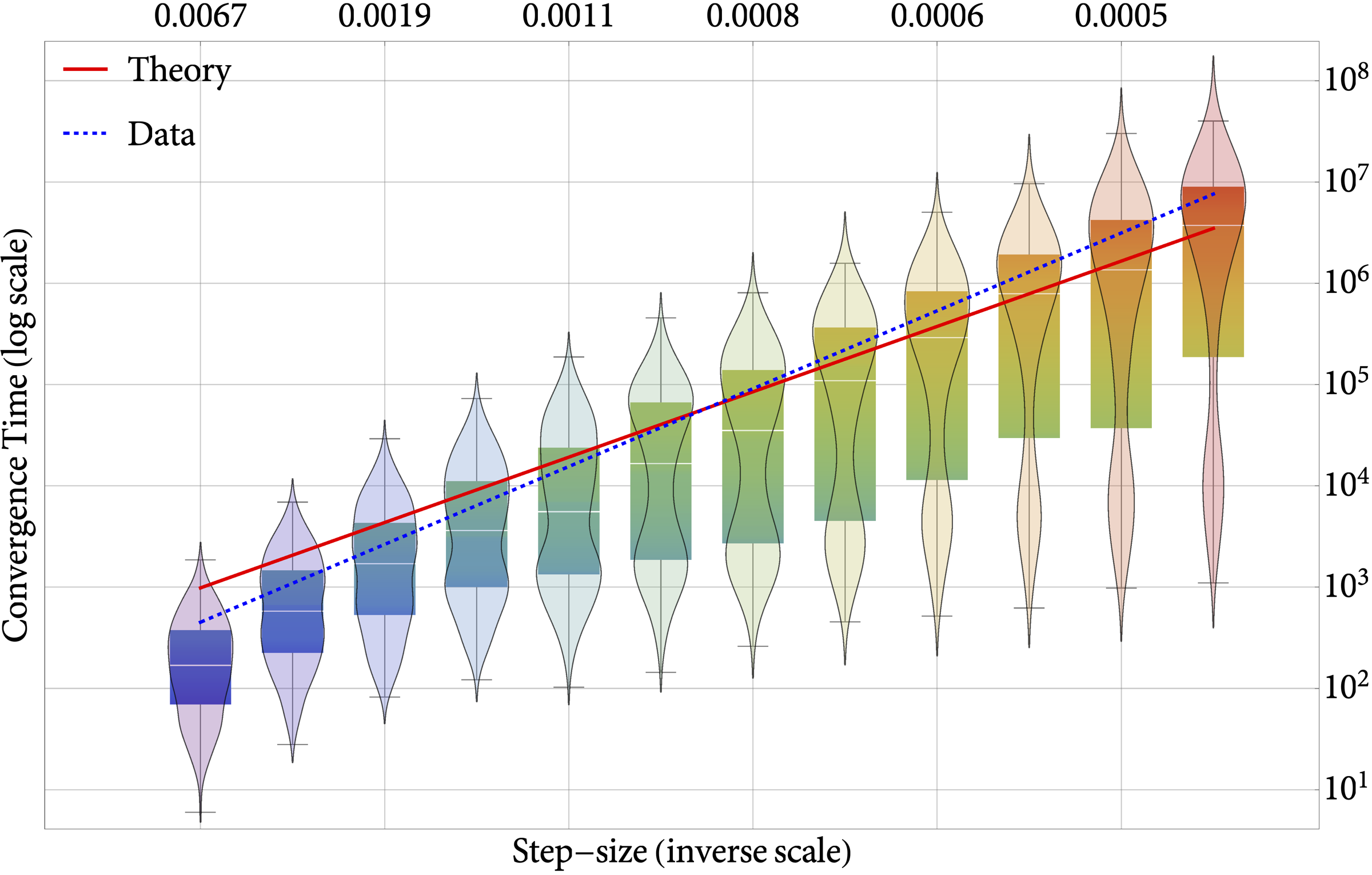
Figure: The global convergence time of SGD as a function of the step-size (right) in the three-hump camel test function (left).