[C58] - Online non-convex optimization with imperfect feedback
A. Héliou, M. Martin, P. Mertikopoulos, and T. Rahier. In NeurIPS '20: Proceedings of the 34th International Conference on Neural Information Processing Systems, 2020.
Abstract
We consider the problem of online learning with non-convex losses. In terms of feedback, we assume that the learner observes – or otherwise constructs – an inexact model for the loss function encountered at each stage, and we propose a mixed-strategy learning policy based on dual averaging. In this general context, we derive a series of tight regret minimization guarantees, both for the learner’s static (external) regret, as well as the regret incurred against the best dynamic policy in hindsight. Subsequently, we apply this general template to the case where the learner only has access to the actual loss incurred at each stage of the process. This is achieved by means of a kernel-based estimator that generates an inexact model for each round’s loss function using only the learner’s realized losses as input.
arXiv link: https://arxiv.org/abs/2010.08496
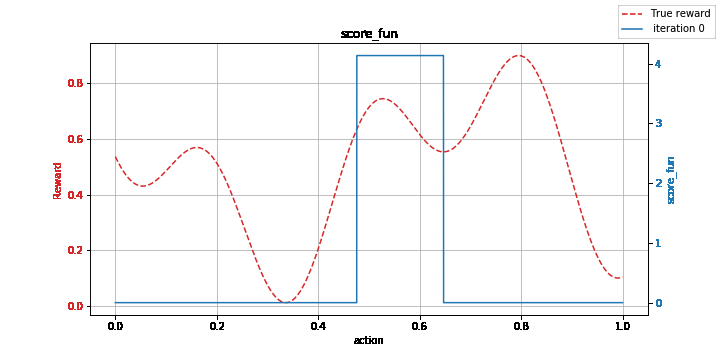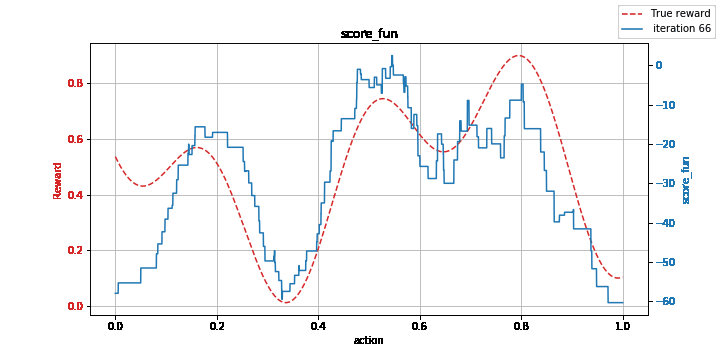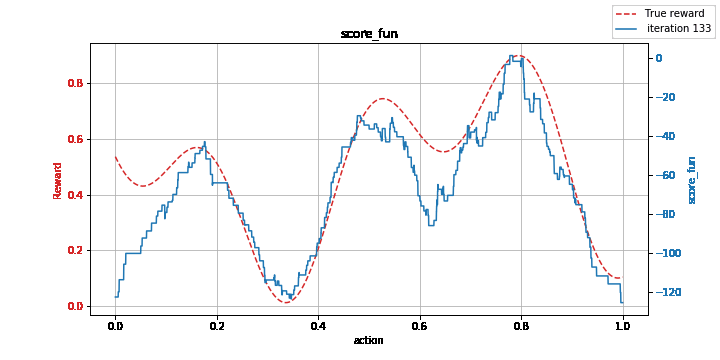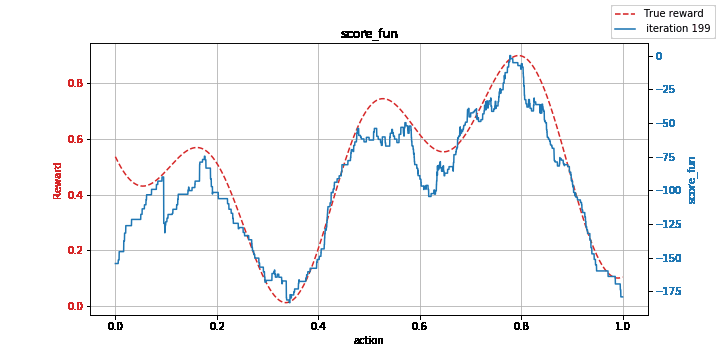
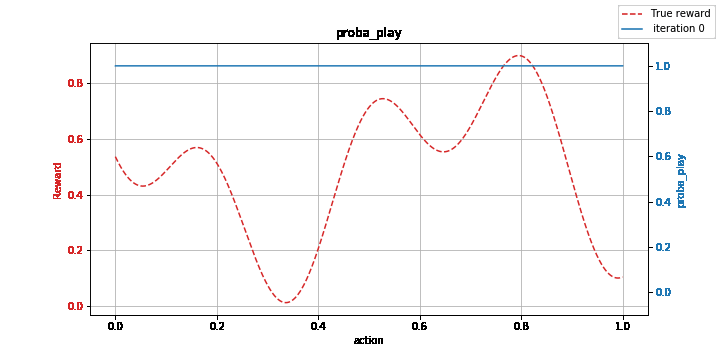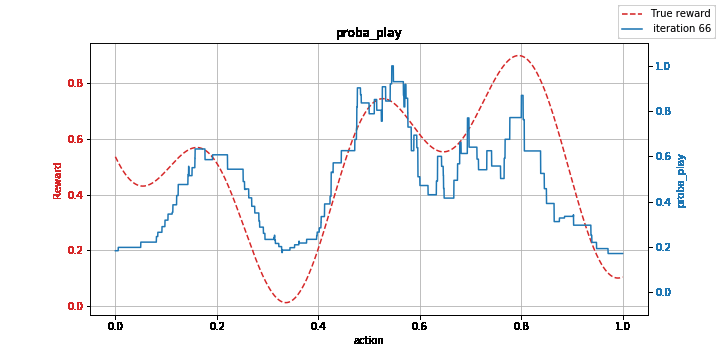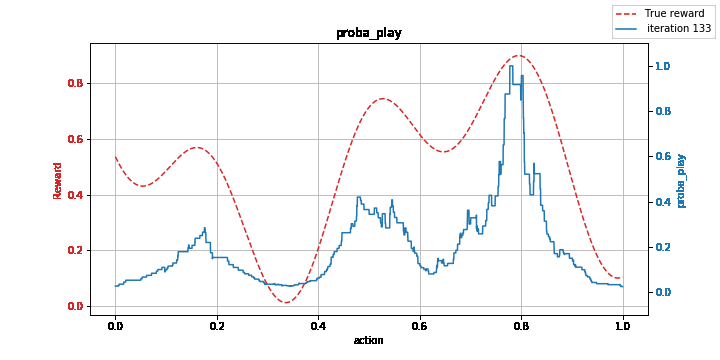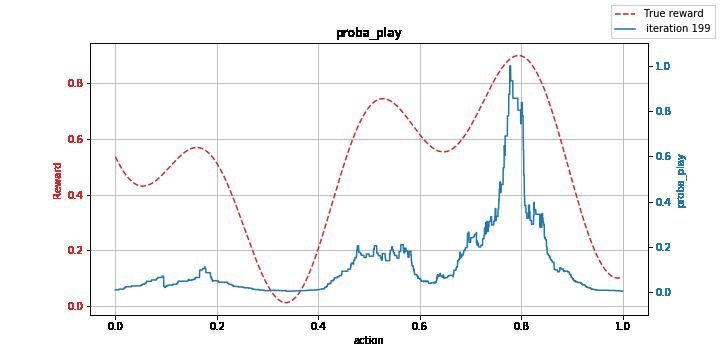
Figure: Learning a non-convex function with the kernelized EXP3 method: model (left) vs. estimation of its maximum (right).