Décomposition de domaine - Méthode de Schwarz

Nicolas Maillard - Eric Blayo

La méthode de Schwarz

Le but de ce mini-projet est de paralléliser la résolution d'une edp. Soit par exemple le problème à deux dimensions suivant : trouver u qui vérifie

 

où f et g sont des fonctions données de dans .

Soit . On définit comme le rectangle et comme le rectangle (cf. la figure 1).

  
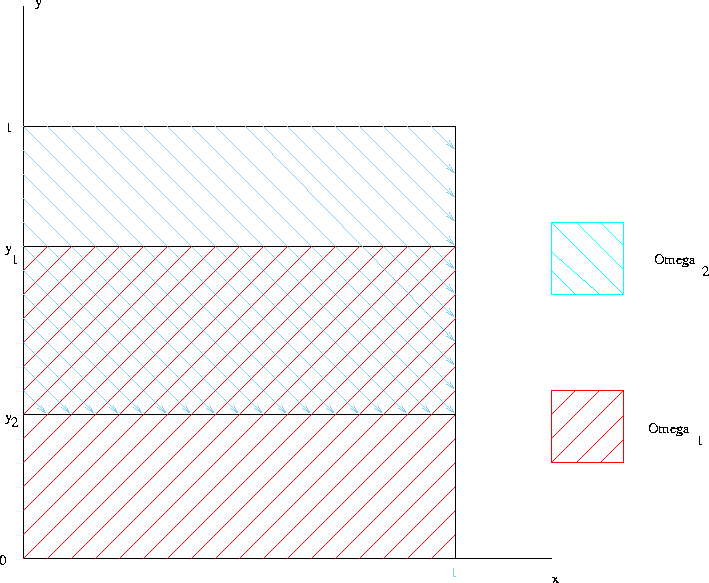
Figure 1: Domaine d'intégration

Le domaine d'intégration est ainsi décomposé en sous-domaines .

La méthode de Schwarz (ici additive) est une méthode itérative. On discrétise le domaine d'intégration (par exemple par différences finies) et la solution à l'itération n sera donc un vecteur à N composantes (où N est le nombre de points de discrétisation). On note la solution sur le sous-domaine .

L'algorithme est alors le suivant : on se donne un vecteur de départ , et on itère les résolutions des sous-problèmes suivants :

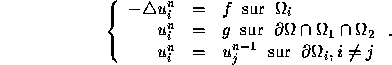
On est donc ramené à 2 (dans notre cas) résolutions de notre edp avec des conditions au bord qui ``forcent'' la régularité de la solution globale. Chaque résolution se fait sur un sous-domaine ``indépendant'' et chaque itération peut donc se faire en parallèle.

Sur un sous-domaine, la résolution du problème se ramène a celle d'un système, lui-même résoluble par exemple par une méthode itérative (gradient conjugué...).

Travail demandé

On pourra refléchir aux point suivants :

• étude de la convergence de la méthode de Schwarz : à 1D ; dans le cas décrit ; en fonction de la largeur de recouvrement entre les domaines (à discuter en tenant compte aussi de la redondance dans les calculs...), en général (?)...
• étude de l'algorithmique numérique à mettre en oeuvre pour résoudre un sous-problème ;
• au niveau parallélisme : solution récursive (divide and conquer), décomposition en p sous-domaines, en P>p sous-domaines avec régulation dynamique de charge ?...
• expérimentation avec des conditions aux bords variées...

Références

1

La page d'E. Blayo de références.