[C59] - No-regret learning and mixed Nash equilibria: They do not mix
L. Flokas, E. V. Vlatakis-Gkaragkounis, T. Lianeas, P. Mertikopoulos, and G. Piliouras. In NeurIPS '20: Proceedings of the 34th International Conference on Neural Information Processing Systems, 2020.
Abstract
Understanding the behavior of no-regret dynamics in general $N$-player games is a fundamental question in online learning and game theory. A folk result in the field states that, in finite games, the empirical frequency of play under no-regret learning converges to the game’s set of coarse correlated equilibria. By contrast, our understanding of how the day-to-day behavior of the dynamics correlates to the game’s Nash equilibria is much more limited, and only partial results are known for certain classes of games (such as zero-sum or congestion games). In this paper, we study the dynamics of “follow the regularized leader” (FTRL), arguably the most well-studied class of no-regret dynamics, and we establish a sweeping negative result showing that the notion of mixed Nash equilibrium is antithetical to no-regret learning. Specifically, we show that any Nash equilibrium which is not strict (in that every player has a unique best response) cannot be stable and attracting under the dynamics of FTRL. This result has significant implications for predicting the outcome of a learning process as it shows unequivocally that only strict (and hence, pure) Nash equilibria can emerge as stable limit points thereof.
arXiv link: https://arxiv.org/abs/2010.09514
[Spotlight talk at NeurIPS 2020]
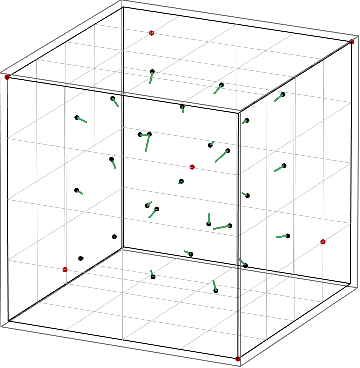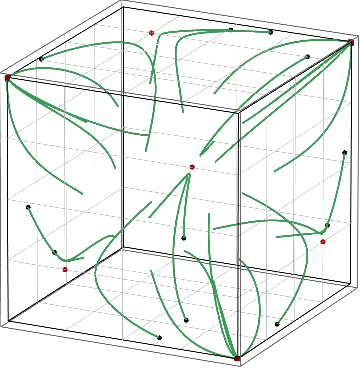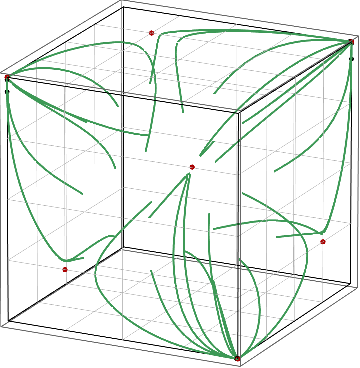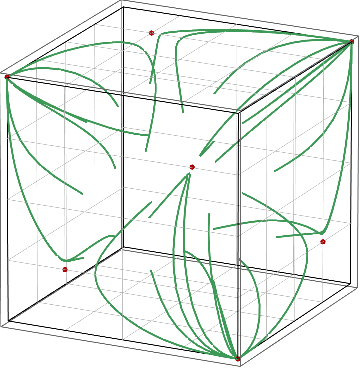
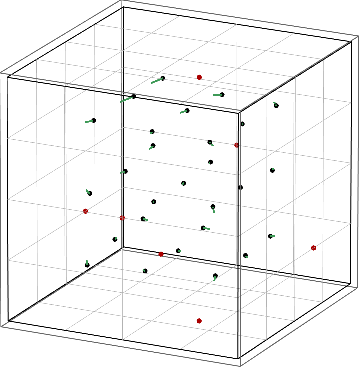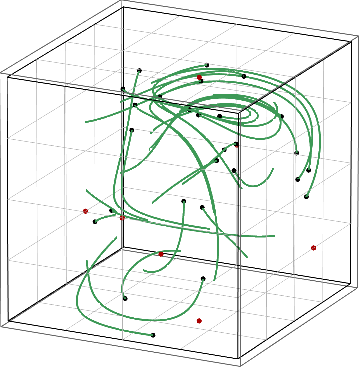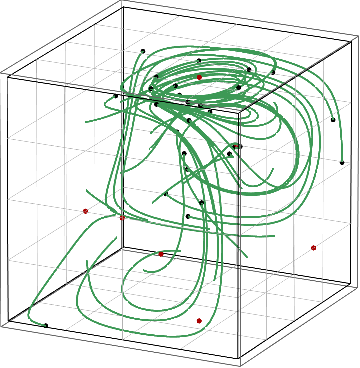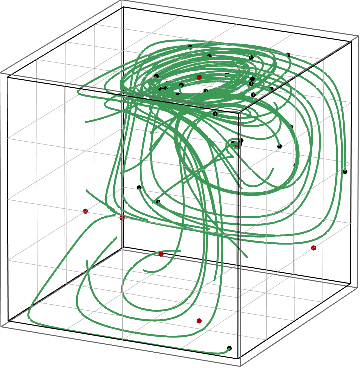
Figure: Convergence of no-regret learning to strict Nash equilibria (left) vs. avoidance of mixed Nash equilibria (right).