[C64] - The limits of min-max optimization algorithms: Convergence to spurious non-critical sets
Y.-P. Hsieh, P. Mertikopoulos, and V. Cevher. In ICML '21: Proceedings of the 38th International Conference on Machine Learning, 2021.
Abstract
Compared to minimization problems, the min-max landscape in machine learning applications is considerably more convoluted because of the existence of cycles and similar phenomena. Such oscillatory behaviors are well-understood in the convex-concave regime, and many algorithms are known to overcome them. In this paper, we go beyond the convex-concave setting and we characterize the convergence properties of a wide class of zeroth-, first-, and (scalable) second-order methods in non-convex/non-concave problems. In particular, we show that these state-of-the-art min-max optimization algorithms may converge with arbitrarily high probability to attractors that are in no way min-max optimal or even stationary. Spurious convergence phenomena of this type can arise even in two-dimensional problems, a fact which corroborates the empirical evidence surrounding the formidable difficulty of training GANs.
arXiv link: https://arxiv.org/abs/2006.09065
[Oral (long talk) at ICML 2021]
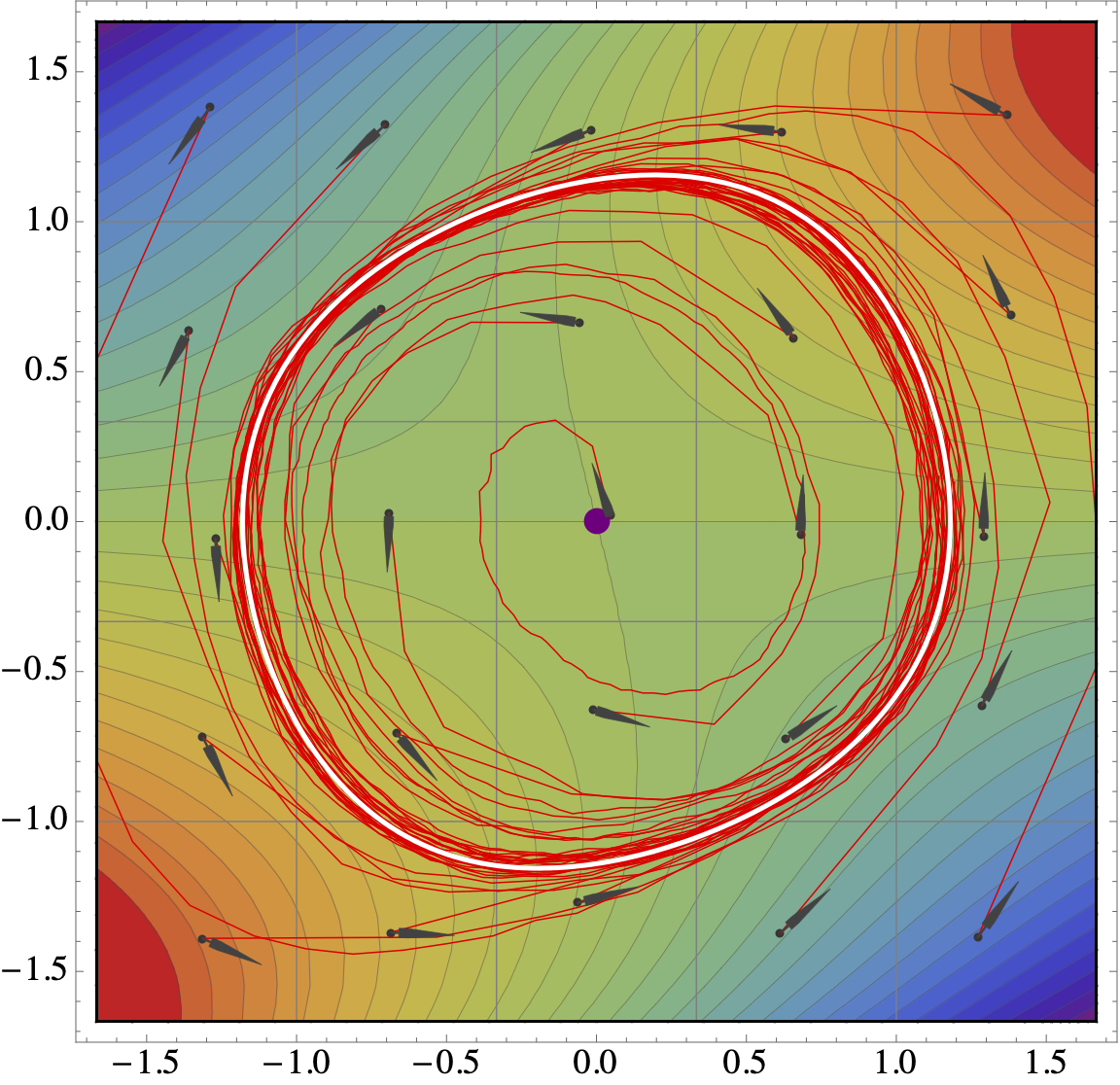
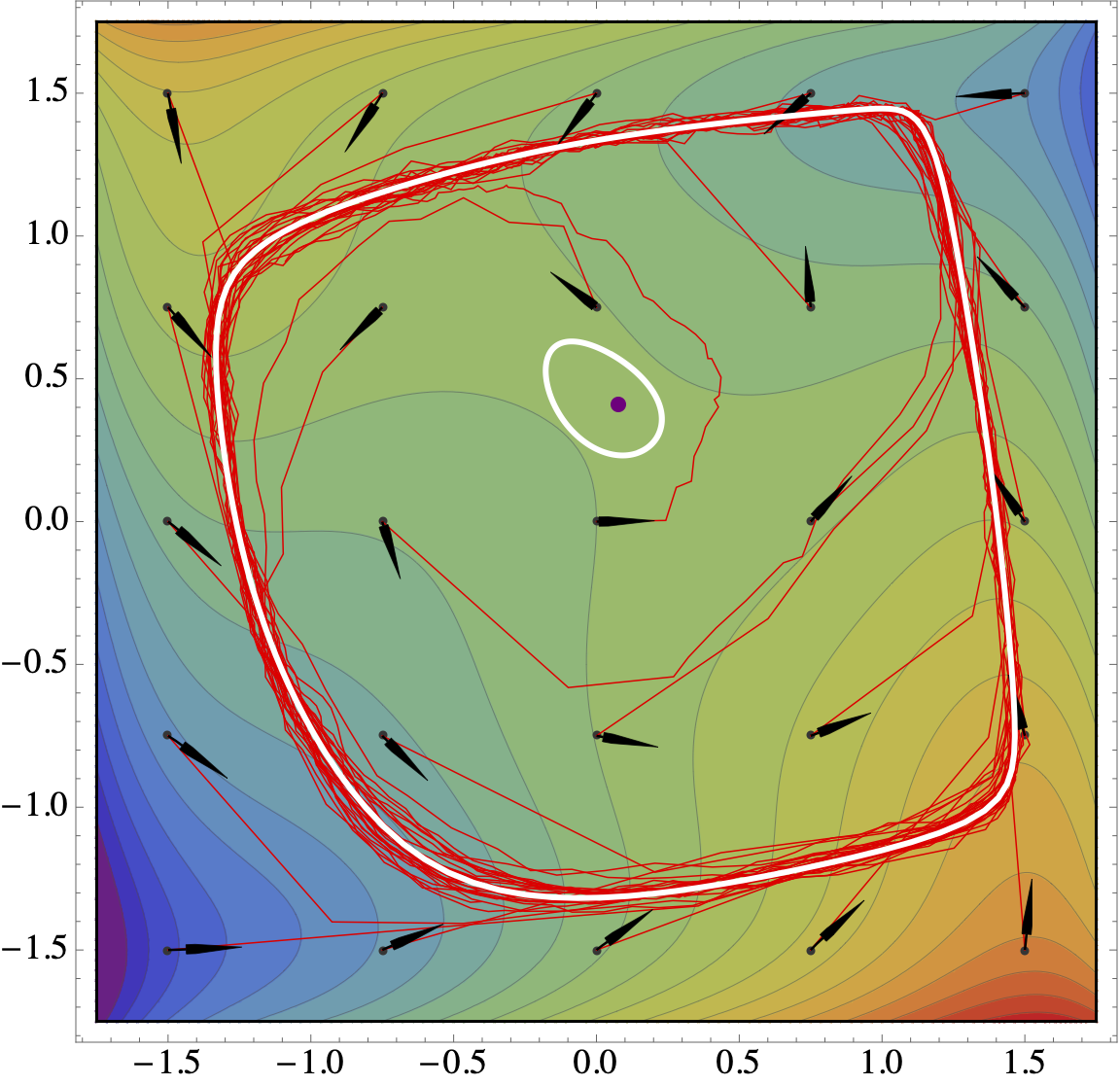
Figure: Illustration of Robbins-Monro algorithms being trapped by (unavoidable) spurious cycles in a $2$-dim min-max game.