Biographical information
For the bullet-point version: see my CV.
As an undergrad, I majored in physics at the University of Athens. After graduating in 2003, I enrolled in the graduate program of the Mathematics Department of Brown University. While there, I worked on differential geometry with George Daskalopoulos and I got my M.Sc. and M.Phil. in Mathematics in 2005 and 2006 respectively.
My interests subsequently shifted to applied mathematics and theoretical computer science, so I returned to the University of Athens where I started my PhD with Aris Moustakas. During my PhD, I worked on the applications of game theory to network science and I completed my thesis on “Stochastic perturbations in game theory and applications to networks” in 2010. Subsequently, I spent 2010–2011 as a post-doc at the École Polytechnique in Paris, working on game theory and learning with Rida Laraki.
Since 2011, I have been affiliated with the French National Center for Scientific Research (most recently as a research director in the joint Inria/LIG team POLARIS), as a visiting scholar / professor at the LUISS University of Rome, UC Berkeley, EPFL and NKUA, and as a collaborating senior researcher at the Archimedes Research Center.
In 2019, I completed my Habilitation à Diriger des Recherches (HDR) on “Online optimization and learning in games: Theory and Applications”. If you are curious, you can find here the transcript of my public defense and the referee reports by Jérôme Bolte, Nicolò Cesa-Bianchi, and Sylvain Sorin (to whom I am deeply indebted for their time).
My recent work revolves around game theory, optimization, and their applications to machine learning, operations research, and data science… and I’m still as liable as ever to drop what I’m doing when faced with a cute little problem!
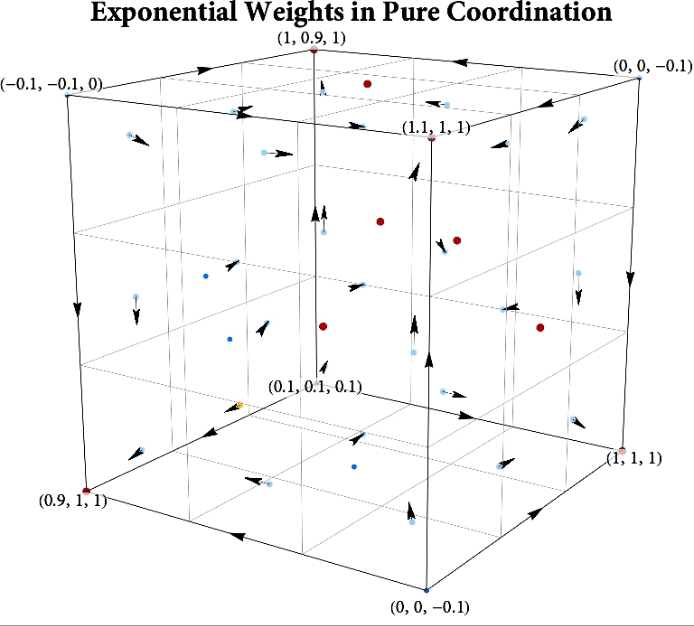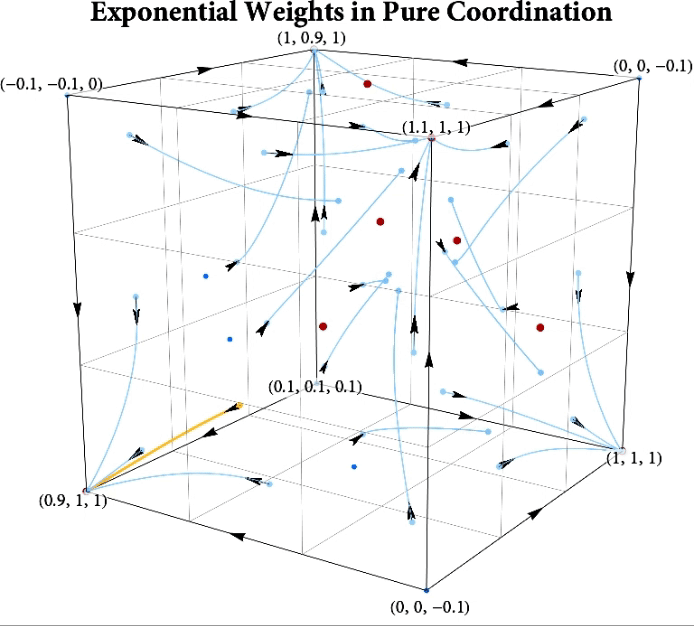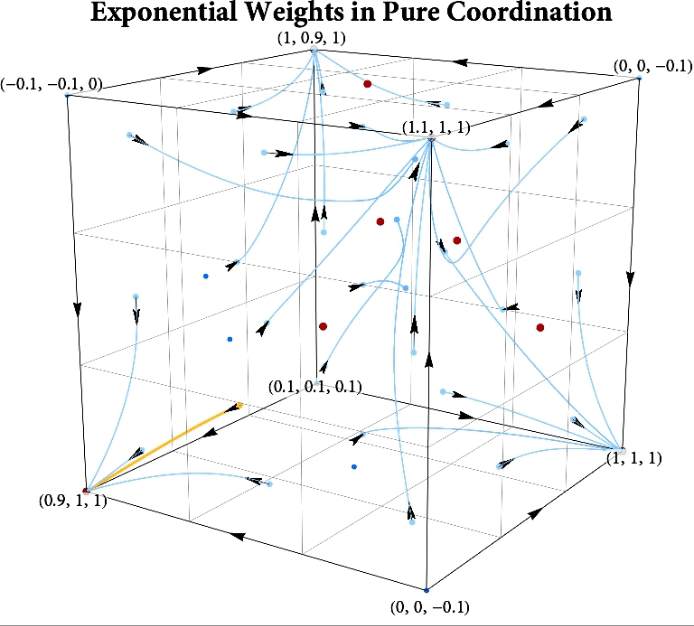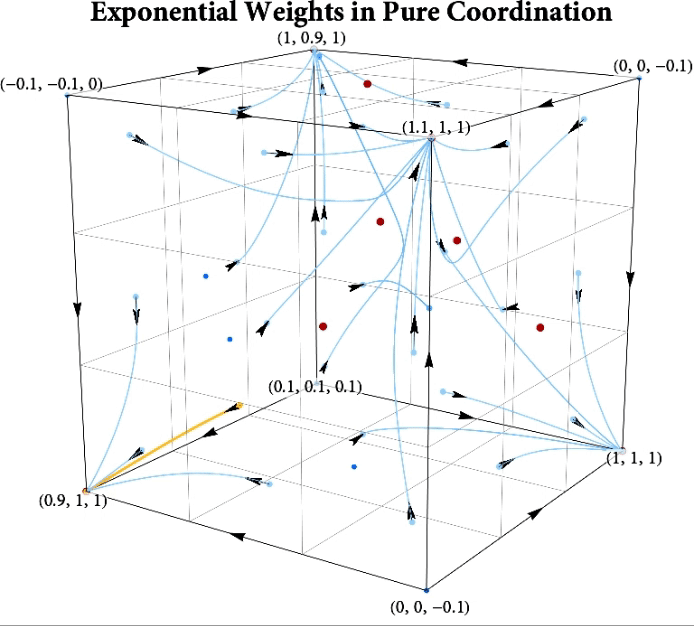
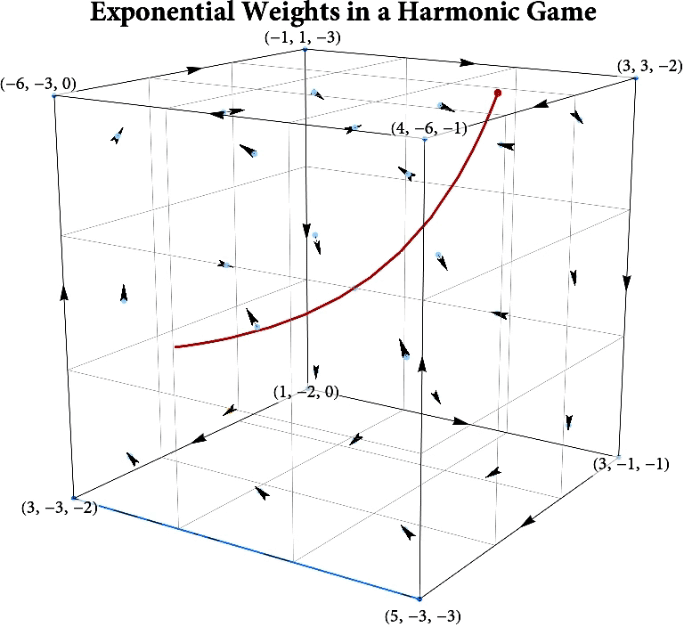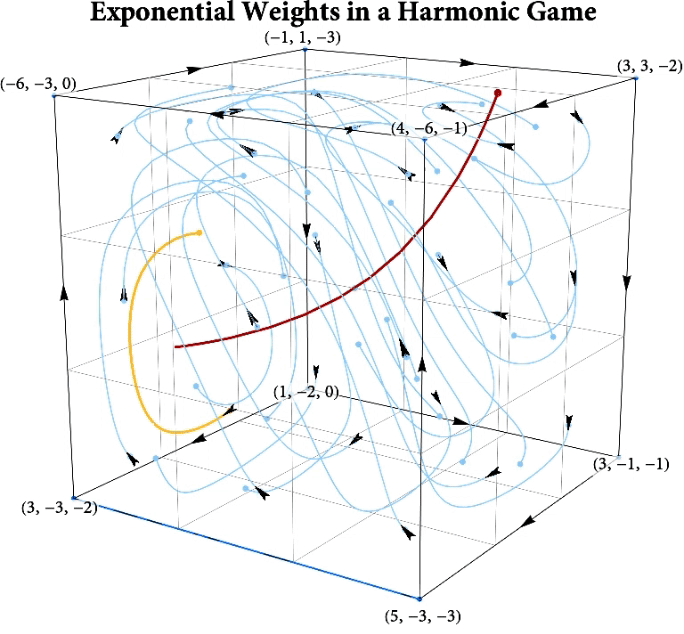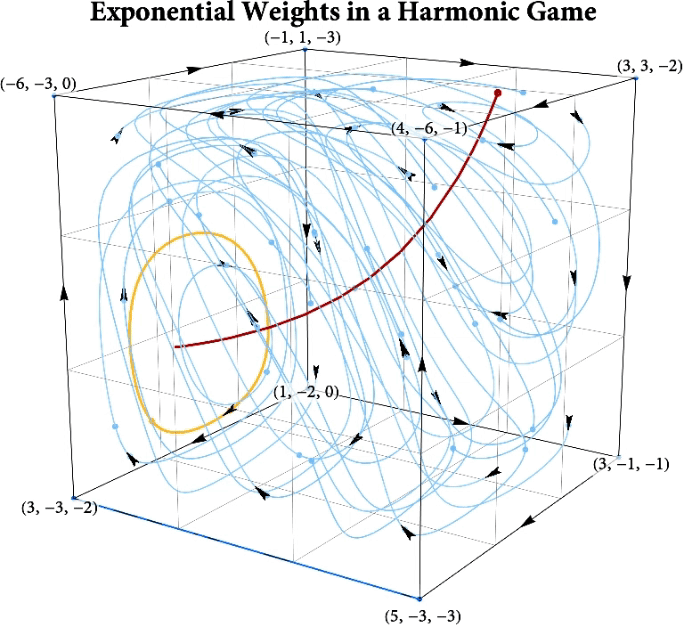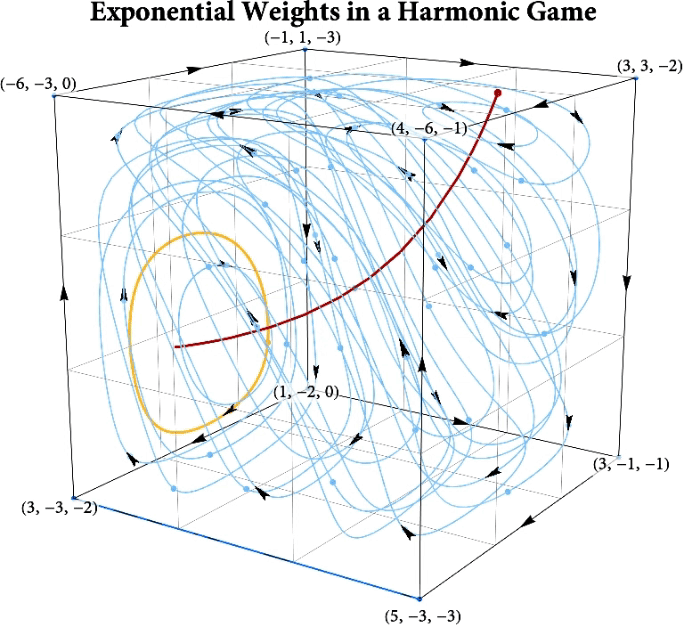
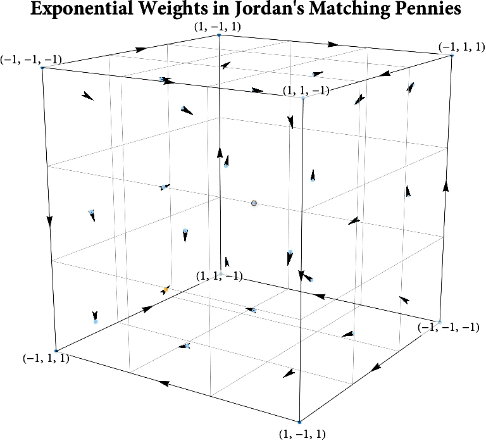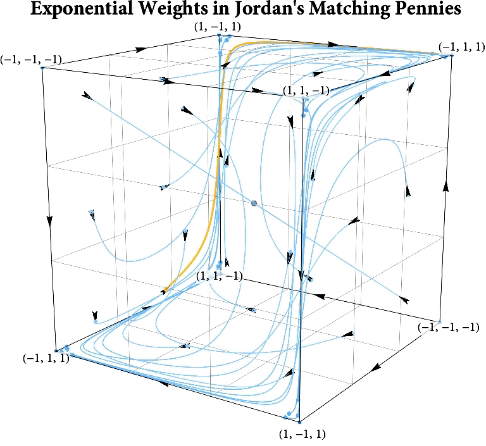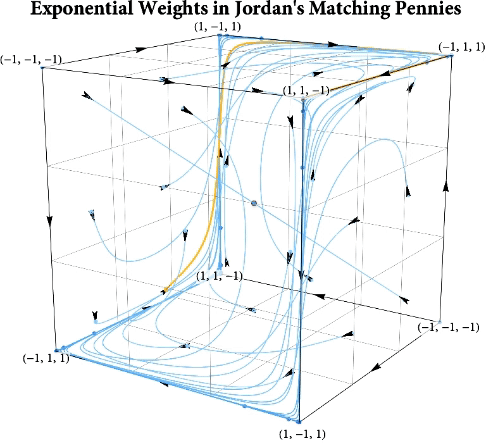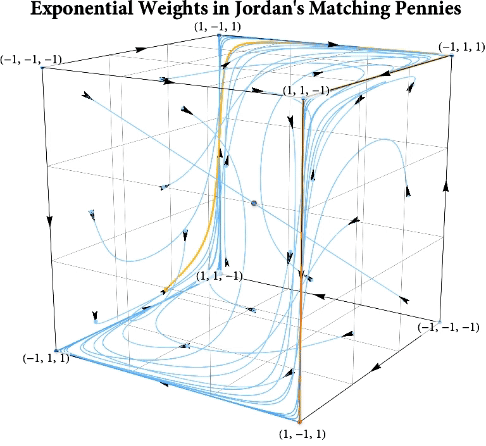
Figure: The long-run behavior of the exponential weights algorithm in different games (click plot to replay). The theory can be found here.